學習筆記 | 零知識證明算法之PLONK——電路_CRS

最近研究了下零知識證明算法-PLONK。肚子里的墨水又增加了，記一下學習成果與新的體會，和大家共同學習---江小白。

現狀

近些年，各種新的零知識證明算法層出不出，各有各的特點，各有各的優勢。借用V神系列文章里的一張圖來簡單呈現下當前的零知識證明算法現狀。

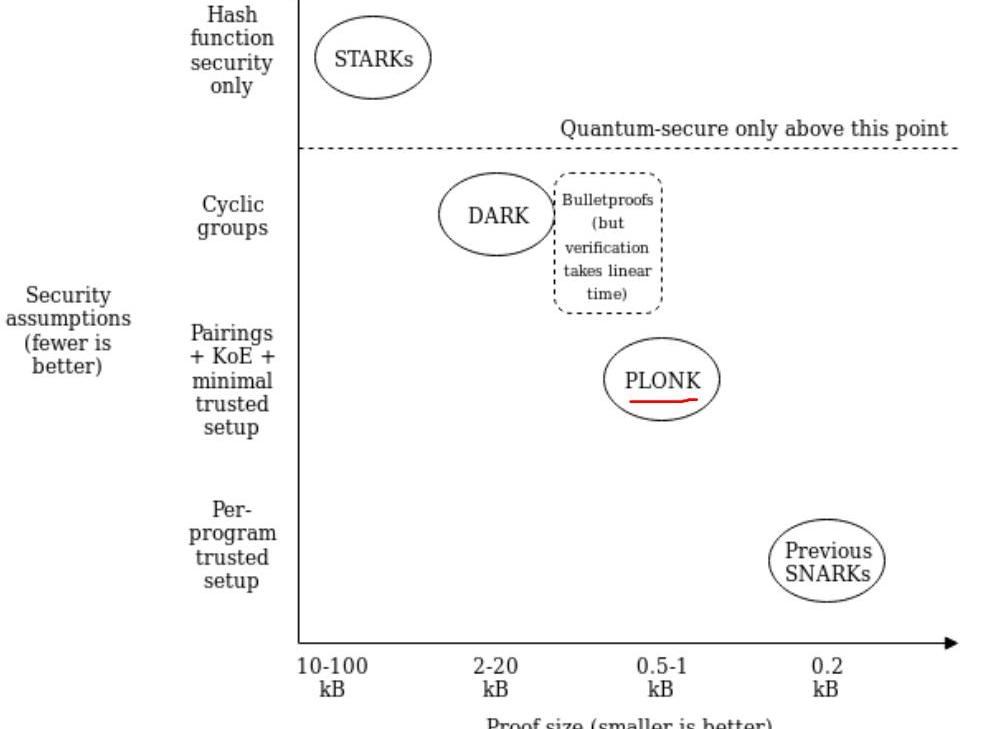
從圖中可以簡單總結出以下幾點：

理論上安全性最高的是STARKs算法，不依賴數學難題假設，具有抗量子性；Proof大小上最小的是SNARKs算法，如Groth16;PLONK算法在安全性上和Proof大小上，位于上述兩者之間；其他的這里不做過多闡述，如想了解零知識證明更多信息，可參考鏈接；對于SNARKs算法，繞不開的一個點就是中心化的TrustSetup，也稱之為CRS(theCommonReferenceString)。而無論是PGHR13,Groth16,還是GM17算法，它們的CRS都是一次性的，不可更新的。即，不同的問題將對應著不同的CRS，這在某些場景下，會變得比較麻煩。這些存在的問題，變成了PLONK，SONIC這類算法的一個優勢，它們算法雖然也需要中心化的可信設置，但是它的CRS具有一定的普適性。即，只要電路的大小不超過CRS的上限閾值，一些證明問題就可以共用一個CRS，這種CRS稱之為SRS(universalStructuredReferenceString)，關于SRS的定義，詳細的可參考SONIC協議里的第3小節。PLONK算法繼用了SONIC算法的SRS的思想，但是在證明的效率上，做了很大的提升。接下來，讓我們詳細的介紹下PLONK算法的具體細節，主要從下面四個小節去分享：

江西省委書記：各級領導干部要沉下心學習區塊鏈等新興產業相關知識:4月16日，江西省委、省政府召開全省數字經濟創新發展大會，省委書記劉奇出席并講話。他表示，各級領導干部要善于學習借鑒先進地區的好經驗好做法，沉下心學習大數據、云計算、人工智能、區塊鏈等新興產業相關知識，切實提高發展數字經濟的能力水平，努力做數字經濟發展的行家里手。（大江網）[2020/4/17]

電路的設計--描述PLONK算法的電路的描述思想；置換論證或者置換校驗--復制約束，證明電路中門之間的一致性；多項式承諾--高效的證明多項式等式的成立；PLONK協議--PLONK協議剖析；電路

PLONK算法電路的描述和SONIC算法一直，具體的過程可以參考李星大牛的分享，已經寫的比較詳細且易懂。在這個小篇幅里，我想主要分享下我自己的兩點想法：

無論是什么樣的電路描述方式，電路的滿足性問題都要歸結于2點，門的約束關系和門之間的約束關系成立；在SNARKs系列的算法里，電路的描述單元都是以電路中有效的線為基本單元，具體的原理可以參考我之前分享的文章，而在PLONK，SONIC以及HALO算法里，電路的描述單元都是以門為基本單元。這兩種電路的不同描述方式帶來了一定的思考。那就是，之前在研究SNARKs算法時，我們都已經相信一個事實，“多項式等式成立，就代表著每個門的約束成立”，然后推斷，整個電路邏輯都是成立；在這個過程中，并沒有額外的去證明門之間的一致性成立；但是在PLONK算法里，除了要證明多項式等式成立外，還要額外的用置換論證的數學方法去證明門之間的約束關系，即復制約束。為何會有這樣的區別？希望有心的讀者能一起在評論區探討這個問題？我個人理解是因為電路的描述方式的不同：

動態 | 百度推出在線學習資源 包括區塊鏈方向課程:新型冠狀病疫情防控正處于關鍵時期，為了確保廣大師生停課不停學，從2月1日起至2月8日，百度云智學院所有在線學習資源都可以在官網免費獲取。包括人工智能、深度學習、虛擬現實、區塊鏈、物聯網等多個前沿技術方向的專題課程，還有Python等編程語言全棧課程。（新浪教育網）[2020/2/1]

PLONK算法里，電路描述的單元是門，它為每個門定義了自己的L,R,O，因此需要證明門之間的一致性；SNARKs算法里，電路描述的單元是線，門與門之間的值用的是同一個witness，因此不用額外證明一致性；置換論證

前面我們說過，在PLONK算法里，需要去證明門之間的約束關系成立。在做具體的原理解釋之前，我們先簡單的過一下PLONK協議的過程，如下圖所示：

可描述為：

根據電路生成三個多項式，分別代表這電路的左輸入，右輸入，輸出；利用置換校驗協議，去證明復制約束關系成立；步驟3和4，校驗門的約束關系成立。其中第1點已經在電路小節里闡述過了，接下來，將詳細的講解多項式置換校驗的原理。先從簡單的場景去講解：

動態 | Stellar加入Coinbase Earn學習平臺:據coingape報道，Stellar加入了Coinbase Earn學習平臺。Stellar發展基金會將提供價值約1億美元的Stellar作為參加該平臺學習計劃的用戶的獎勵。[2019/3/27]

單個多項式的置換校驗

其實就是證明對于某個多項式f，存在不同的兩個點x,y，滿足f(x)=f(y)。下面來看具體的原理：

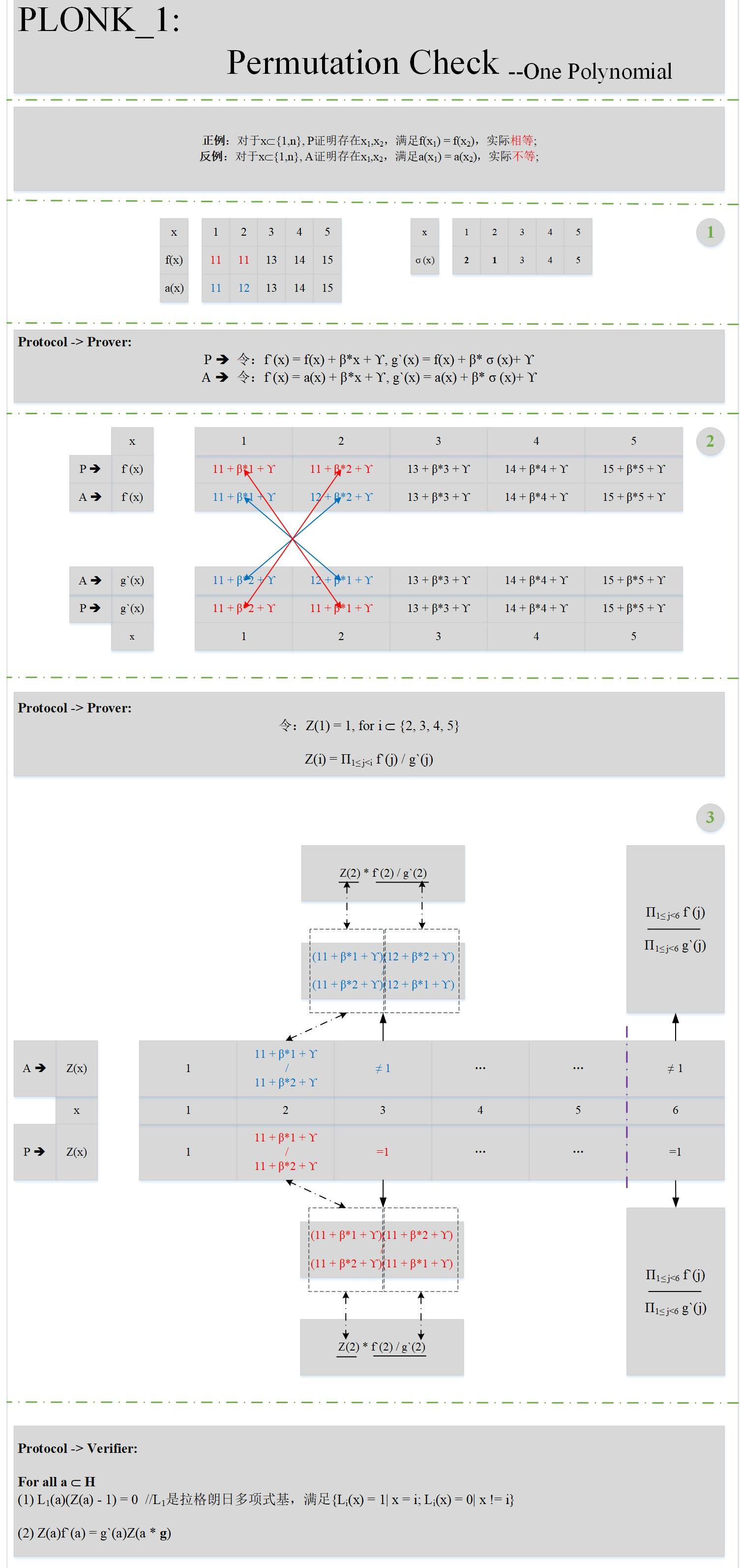
上圖中加入了一個正例P，一個反例A，方便大家理解置換校驗的原理。有幾點需要解釋的是：

而經過仔細剖析Z的形式，不難發現，Z(n+1)其實就是兩個函數所有值的乘積的比值(不知是否等同于V神文章里的坐標累加器？)。理論上是等于1。因此，我們需要設計這樣的一個多項式Z，需滿足：deg(Z)<n

現場 | 鮑帥：機器學習技術能極大提升智能合約安全檢測引擎效率:金色財經現場報道，今日，2018可信區塊鏈峰會在北京召開。在主題為“區塊鏈安全焦點關注”的區塊鏈安全論壇上，西安好碼安全信息科技有限公司CEO鮑帥分析了智能合約與機器學習的相互影響。他指出，當前智能合約發展迅速，如何有效處理海量智能合約的安全成為行業普遍關注的問題，機器學習技術的引入能極大地提升智能合約安全檢測引擎效率，在大規模 、易擴展、半監督學習、高價值、高效率、通用方案等方面發揮較大的優勢。[2018/10/10]

Z(n+1)=1

2.乘法循環群剛好可以滿足這個條件，如果設計一個階為n的一個乘法循環群H，根據群的性質可以知道Z(g)=Z(g^(n+1))。因此，在設計Z時，會保證Z(g)=1；上圖中的自變量的取值也將從{1...n}變成{g...g^n}。所以在上圖中驗證的部分，a其實已經換成了群H里的所有元素。

3.根據論文中的協議，多項式Z是會發給可信第三方I驗證方V會從I處獲取到多項式Z在所有a處的取值，然后依次校驗。

美國國會代表Tom Emmer：美國應該向日本學習加密貨幣監管:本周盛頓區塊鏈峰會，美國國會代表Tom Emmer告訴coindesk：“如果監管機構的管理過度擴張，區塊鏈和加密貨幣的變革的能力將永遠不會實現。” Emmer表示，通過學習日本在加密貨幣監管方面的舉措，美國可以做到更好。目前日本只有一個監管機構——金融服務局對加密貨幣擁有管轄權。他認為作為一個機構，應該知道要向哪個方向發展，知道誰負責，知道問題是什么，并且必須做出回應。目前政府監管并不是唯一能夠澄清和確定加密貨幣規則的方法。他表示，實際上加密貨幣行業可以提供很多監管，然后立法人員應該認識到我們希望行業能夠盡其所能。Emmer最后表示，他認為區塊鏈的未來是光明的，但是政府部門必須十分小心。[2018/3/10]

下面具體看一下論文中的定義：

從定義中可以看出：多項式f,g在范圍內具有相同的值的集合；下面看一下論文中具體的協議部分，結合上述解釋的3點：

說明：圖4中的f,g對應圖3中的f。即f,g是同一個多項式。其實只要是相同的值的集合，也可以不用于是同一個多項式。圖3是一個特例而已。

跨多項式的校驗

其實就是證明對于某個多項式f，g，存在兩個點x,y，滿足f(x)=g(y)。與存在兩處不同：

多個多項式；不強制x,y的關系，即也可以等，也可以不等；有了(1)小節的基礎，這次我們先看一下相關的定義：

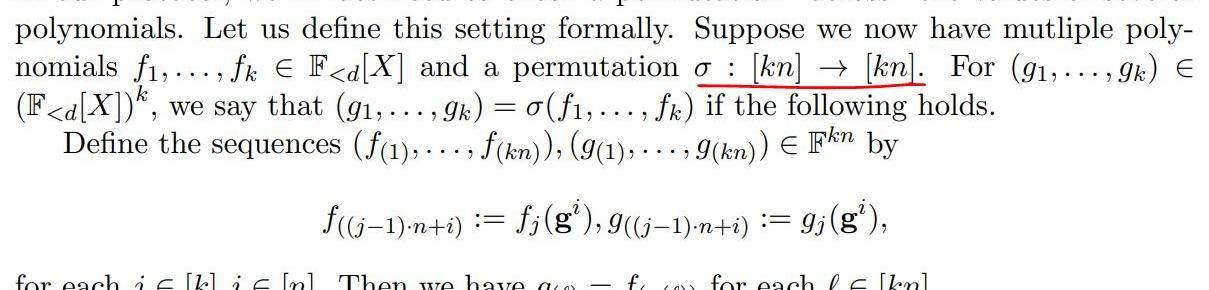
從定義可以看到，這次是兩個多項式集合見的置換校驗算法。從標注的部分可以看出：

兩個多項式集合仍然具有相同的值的結合；為了區分集合里的多項式，自變量的索引得區分開來；因此，可以想象的到，如果存在兩個多項式f,g，想要證明f(x)=g(y)，那么根據以上描述可以判斷{f1,f2}={f,g}={g1,g2}。也保證了上述第1點的成立。

下面我們看一下具體的原理：

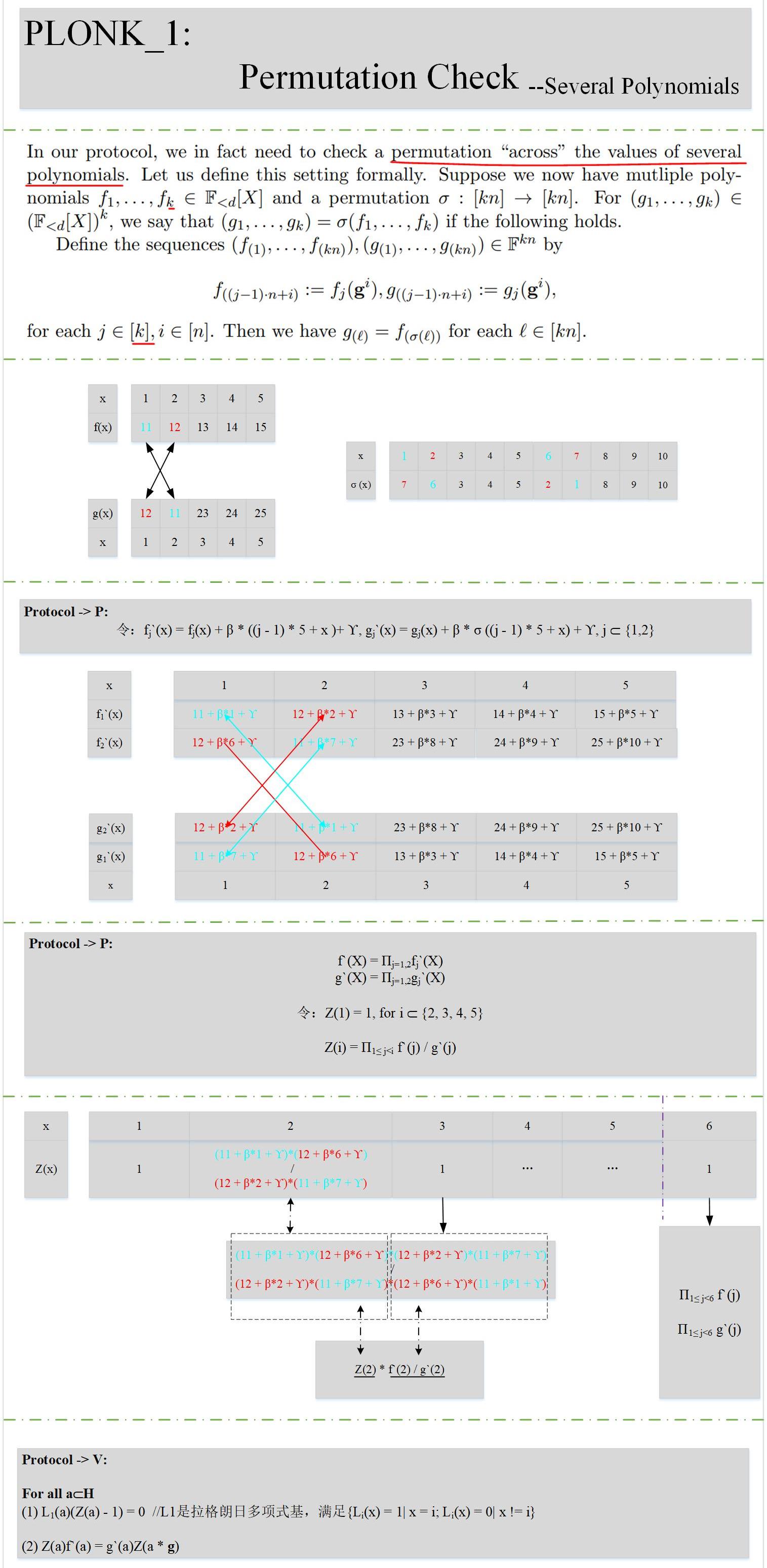
和(1)小節相比，證明方P增加了些工作量，驗證方V工作量不變。結合上述描述，也能很容易的理解其數學原理。

說明：至此，其實我們已經慢慢的接觸到PLONK算法的核心了，前面我們講到，電路的滿足性問題除了門的約束關系還有門之間的約束關系。

比如一個輸入x，它既是一個乘法門的左輸入，又是另外一個乘法門的右輸入，這就需要去證明L(m)=R(n)，這就是跨多項式的置換校驗。

下面再給出論文里的協議內容：

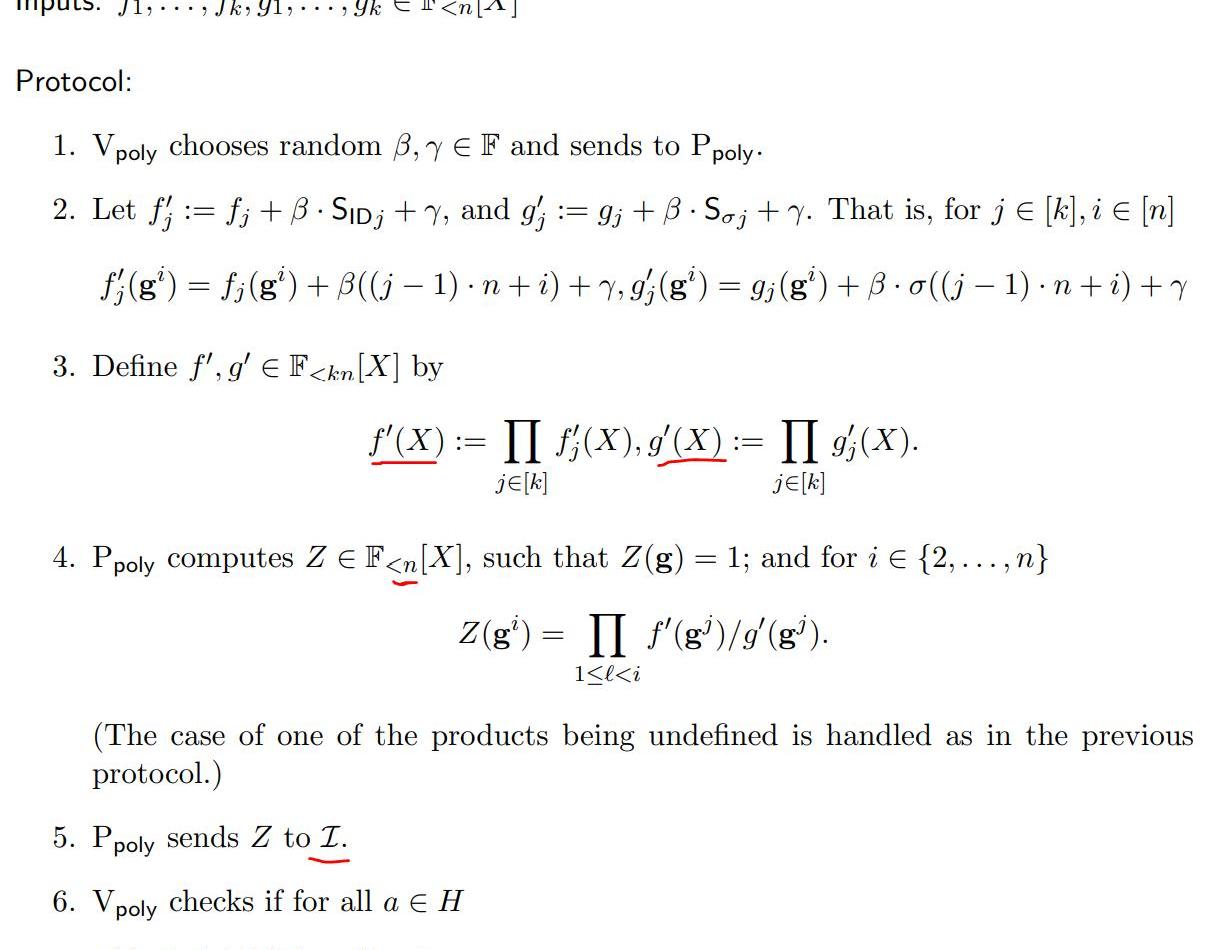
至此，本篇文章已經描述了，在PLONK算法里，電路的設計以及復制約束的成立驗證兩大部分，接下來，將會另起一片文章，去分享門約束的成立和整個協議的具體步驟。

以上都是作者小白的個人理解，還希望各位讀者多多指教，謝謝。

Tags：PLOLON區塊鏈CRSPLOW幣Echelon Prime區塊鏈域名的用途crs幣是什么意思

火幣交易所