雙向復利神奇_馬斯克

我的目的不是為了幫大家溫習數學，而是探索以下重要且有趣的話題：

1、聰明的試錯，是一個逆向復利的過程，它可以幫助我們以指數增長的速度，逆向逼近正確答案；

2、絕大多數成就的取得，都是通過復利效應實現的。但是，復利很難。本文我將講述復利的雙向測試，為靠譜的復利搭建一個可計算的腳手架；

3、兩頭求極限，才是馬斯克的“第一性原理”中最重要但卻被忽略的部分。

4、凱利公式給出了一個最大收益與下注比例之間的數學關系。該公式是在基于概率的復利公式的基礎上，通過取對數然后求導得出的；

5、既然說到了對數，自然要說一下神奇的自然對數e，以及自然增長的極限。

以可感知的方式來重溫對數，能幫助我們從底層理解這個世界的算法。

log10(10)

《魷魚游戲》中的第五關，是“跳玻璃橋”。

有16位選手按照順序過一條玻璃橋。玻璃橋由18節構成，每節有左右兩塊玻璃，一邊是普通玻璃，一邊是強化玻璃。

游戲規則是：參賽者必須正確分辨出普通玻璃和強化玻璃，若踩到普通玻璃就會當場摔死，一路踩到強化玻璃才能過關。

二選一，即使靠蒙，勝率也高達50%。

然而，雖然每一節的變化只有2，兩節的變化也就是22，連續18節的變化是2的18次方，卻高達262144種。

這是一個指數級的增長。

要想連續18次都蒙對，成功的概率是分之一，也就是約為30萬分之一，約為死于從樓梯上摔下來概率的二分之一。

然而，在《魷魚游戲》里，最終有三個人過關，除了靠玻璃廠師傅肉眼辨別出來的較少環節，主要都是以人命為代價蒙出來的。

理論上，如果人們不自相殘殺，即使是靠蒙，活下來的人也應該多于三人。

為什么一個成功率只有近三十萬分之一的游戲，僅僅靠十幾個人就能打通關呢？

因為這是18個串聯在一起的二選一，18個人用命去蒙，相當于一個逆向的指數效應，可以用非常有限的測試，來找到262144種可能性中唯一正確的可能性。

我稱之為：逆向復利。

如各位聰明讀者都知道但可能早已忘記的數學，玻璃橋游戲的巨大不確定性是來自指數增長，而消除不確定性則是靠指數函數的反函數：

對數函數。

log10(100)

先來玩兒一個簡單游戲：

已知有兩個抽屜，各有一黑一白兩個盒子，一共四個。其中一個盒子里有顆大鉆石，猜中了就歸你。你可以問任意問題，主持人必須回答，但只能說“是”或者“不是”。請問你最少要問幾次？

也許你在宿舍生活時，玩兒過類似的游戲：通過不斷問問題，獲得“是或不是”的反饋，然后一步步解出謎題。

答案是你需要問兩次：

第一次：是在左邊的抽屜里嗎？

第二次：是在黑色的盒子里嗎？

這是一個簡化版的“過玻璃橋”游戲。

有算法的瞎蒙，有時候并不蒙瞎。

近300年前，牧師貝葉斯設計了一個思想實驗：

他背對一張桌子坐著，桌子上有個白球，他并不知道白球的位置。

然后，他讓助手隨機往桌面上扔黑球，黑球落在桌子上的位置完全是不確定的；

接下來，每放完一個，他就問助手白球相對于黑球的方位。比如，助手說白球在黑球的右邊，他就猜也許白球在靠右一點兒的位置；

然后，助手又隨手扔了一個黑球，并且告訴他這個白球是在黑球的左邊。于是他更新了猜想，可能白球并沒有那么靠右；

Solana Pay上線交易請求功能，可實現商家和消費者之間的雙向交互:5月5日消息，Solana 發推稱其支付協議 Solana Pay 現已上線交易請求功能，可實現商家和消費者之間的雙向交互，目前可以通過結賬應用和移動錢包之間的交互請求將任何 Solana 交易帶入現實世界，從而實現 NFT 鑄造、動態折扣、代幣化忠誠度計劃等。

此前消息，2 月份，Solana Labs 宣布推出 Solana Pay 支付協議，使得商家可以直接從消費者處接受加密支付，目前支持穩定幣 USDC、Solana 的原生代幣 SOL 以及其他基于 Solana的代幣。[2022/5/5 2:51:36]

就這樣，扔的黑球越多，他就越能逼近白球真正的位置。

這個“無聊”的游戲靠譜嗎？

該實驗中，僅用模糊的相對關系，就能逐步推斷出結果。關于這一點，我會另外在一篇《逆風而行》的文章中再談及。

事實上，貝葉斯的這個思想實驗，是對休謨的因果懷疑論的反擊。結果，產生了一種“由果推因”的逆概率計算，迄今仍在深刻改變這個世界。

也許你會覺得，這種瞎猜，要猜到什么時候？

和過玻璃橋一樣，貝葉斯的計算，也有一種逆向的指數效應，能夠快速逼近白球的真正位置。

log10(1000)

在過玻璃橋游戲里，每一節的變化是2，連續18節的變化，就是2的18次方，這是一個指數運算。

計算結果，是262144種變化。

那么，如果我們只知道一共有262144種變化，但不知道玻璃橋有多少節，該如何計算呢？

這就是指數運算的逆運算：對數運算。

如果a的x次方等于N，那么數x叫做以a為底N的對數，記作x=logaN。其中，a叫做對數的底數，N叫做真數。

對數的意思是：用幾個數與自己乘在一起會得到另一個數？

例如2的三次方是8。那么反過來，多少個2相乘可以得到8？

通過對數運算可知，log2(8)=3。

在過玻璃橋的游戲里，2的18次方等于262144，那么：log2(262144)=18。

指數運算，能夠迅速將一個數字變得非常大；

對數運算，能夠迅速將一個數字變得非常小。

二者放在一起，是一種雙向的“復利效應”。

log10(10000)

關于不怕失敗，主動試錯，已經是老生常談。

《霍亂時期的愛情》里寫道：

“趁年輕，好好利用這個機會，盡力去嘗遍所有痛苦，這種事可不是一輩子什么時候都會遇到的。”

為什么要趁年輕犯錯呢？什么是聰明的犯錯呢？

記得有位科學家說過：所謂專家，就是在一個極小的范圍內犯過了所有的錯誤。

以下圖為例：

你要找尋圖形中藏寶的小方塊，即使你只能像過玻璃橋那樣去試，一次猜一半，你也會以非常快的速度逼近寶藏。

但是，要有以下前提：

1、有邊界。即使逆向的指數效應很強大，但也很難解決沒有邊界的問題；

2、有算法。例如過玻璃橋看似殘酷，但其實是由一連串二選一的問題組成，數學上可以計算，能夠不斷逼近答案；

以太坊與Cardano雙向跨鏈橋公測版即將發布:Cardano生態去中心化項目啟動平臺OccamFi宣布以太坊與Cardano雙向跨鏈橋公測版即將發布。該跨鏈橋實現了將以太坊上的ERC20資產和ETH轉換為Cardano鏈上的包裝資產，也可以將Cardano原生代幣（CNTs）與ADA轉換為以太坊上的包裝資產，如此即可在以太坊上使用智能合約啟用CNT，也可以利用低gas費用的Cardano網絡轉移ERC20代幣從而降低成本。

OccamFi表示目前該跨鏈橋是中心化的，未來將通過與其包裝資產的鑄造和托管合作伙伴Bitcoin.com的合作，逐步將其迭代為去中心化產品。[2021/6/16 23:41:41]

3、有反饋。猜對玻璃，活命；猜錯玻璃，死掉。但是對于整個系統而言，假如只是一個游戲，其實猜對或者猜錯，就信息的傳遞而言，是等價的；

4、能遍歷。參與游戲的人不僅要犯掉所有的錯誤，還要能夠在犯錯之后活下來。對創業者而言就是在錢花光之前快速犯錯然后找到活路。

可口可樂公司的CEO詹姆斯.昆西說：“如果我們不犯錯，那就表明我們工作上都不夠努力。”

奈飛的哈斯廷斯認為：“我們必須要冒更多的風險……去嘗試更瘋狂的事情……。”

貝佐斯將極可能是錯誤的“大膽押注”視為實驗品：

“既然它們是一次實驗，那么你肯定就不能提前知道它們會產生怎樣的作用。畢竟實驗究其本身來講就是一件容易失敗的事兒。但只要有幾個巨大的成功就能彌補你所經歷的無數次的失敗。”

然而，所謂“失敗是成功之母”，在我們這個演化的世界里，對絕大多數人而言并不成立。

即使你勇于失敗，不斷探索，假如你的犯錯不夠聰明，不夠隨機，運氣不夠好，成功照樣不會來臨。

聰明而主動的犯錯，需要有邊界、有算法、有反饋、能遍歷，也需要一些瘋狂、隨機和冗余。

哈耶克說：

雖然進化經常被總結成“適者生存”，但推動進化進程的卻往往是不適者。盡管我們總是本能地以為復雜問題需要精心設計的解決方法，但進化卻毫無規劃可言。復雜得驚人的事物是在簡單的過程中涌現出來的：嘗試已有事物的不同版本，剔除失敗，復制成功經驗。

所以，成功學最大的問題是，忽略了那些事后不再發聲的失敗要素，簡化了因果，甚至顛倒了因果，并且認為成功可以被設計，被簡單復制。

log10(100000)

對于人們熱衷于探尋模式和設計因果，哈耶克批評道：

人們總以為自己能設計出這樣或那樣的東西，但實際上，他們對要設計的東西幾乎一無所知，經濟學的獨特職責就是展示人們的這種無知。

哈耶克的這句話，尤其適合應用于教育領域。

教育的目的和意義到底是什么？

以前是為了培養技能，可以上生產線紡紗造車。現在早變了，漫長的求學生涯，是人類社會的一種冗余機制。

對一個孩子而言，在被保護的童年與青少年期間，低成本地去犯人生當中所有可能的錯誤，也許是最有價值的。

所以，如哈耶克所言，教育應該允許孩子通過犯錯，暴露出自己的無知，自己的愚蠢。

可事實呢？犯錯、無知，是學校里最無法容忍的。

于是，可笑的事情出現了：一個人經歷了十幾年的教育，不斷追求如何將這輩子幾乎都不會再用上的知識做到“不出錯”，不斷地將那些嚴絲合縫的因果關系背得爛熟，最寶貴的個性因為無法顯現而被磨滅，無價的多樣性被統一的生產線加工成一個模子。

可是，我們眼前復雜的現實世界，越來越像休謨在幾百年前所說的：

“我們無從得知因果之間的關系，只能得知某些事物總是會關聯在一起。”

Gate.io發布安卓手機及iOS最新版本，支持合約雙向開倉功能:據官方公告，Gate.io發布安卓手機APP V2.6.8.beta及iOS TestFlight 2.5.3版本，新版本合約均支持雙向開倉功能。新用戶可到官網APP下載界面進行下載，老用戶可直接通過左側欄升級。[2020/12/8 14:33:55]

產生于工業革命年代的傳統教育，早已無法應對非線性的、不確定的當下。

如果傳授確定性知識的教育只是成為一個智力測試系統，以摧毀人才的方式來選拔人才，那么這一代價對社會、對個體而言都太昂貴了。

某女子學校創建了一個名為“失敗”的項目。負責人雷切爾·西蒙斯說了一句非常貝葉斯主義的話:

“我們想要告訴大家的是，失敗并不是學習過程中犯的錯誤，而是學習過程中的特征。”

教育教會我們學習和思考，更是教會我們如何挖掘自己獨一無二的寶藏。

大自然實現了某種有算法的隨機性，學校也應該如此。

所謂因材施教，不是定制名表，定制名包，而是提供一個有算法的系統，并且通過模擬真實的現實世界，讓孩子自由探索，大膽犯錯，無所顧忌地暴露自己的無知，呈現自己的天性，從而發現自己的稟賦，點燃愿意終其一生去努力的理想。

接下來，我要通過可逆的指數和對數運算，講到復利的雙向測試。

log10(1000000)

“奇怪”的是，對數的發明先于現代指數。原因是對數當時在航海與天文學領域太實用了。

對數可以將高級運算降為次級運算，例如化乘方開方為乘除，化乘除為加減，從而極大降低了運算量。

指數和對數互為“反函數”，二者之間是可逆的關系。

先看從指數到對數：

我們把k輸入到上面的運算器，經過指數運算，得到a的k次方，再代入對數運算，又輸出了k。

再倒過來，看從對數到指數，一樣是輸入K，輸出k。

如上運算器，我們可以從左邊輸入，右邊輸出；也可以從右邊輸入，左邊輸出。

就像貝葉斯提出的逆概率，從而實現了可以“由果推因”，如上的雙向運算，既是由因推果，又是由果推因。

這種方法，可以幫助我們檢驗自己的信念。

例如，假如你看到：

某人非常聰明并且努力，所以在房地產行業賺到了很多錢。

你就可以做一個雙向測試：

從“非常聰明并且努力”，可以推出“在房地產行業賺到很多錢”嗎？

從“在房地產行業賺到很多錢”，可以推出“非常聰明并且努力”嗎？

如果不能，我們可能需要重新定義自己的那個信念。

以下我要講的，絕非用公式包裝成功學，而是分享一個有趣的“感知”。

我相信，如果你懂得創業，又懂指數和對數，一定能對如下內容會心一笑。

先定義一下，世俗意義上的成功，大多是通過大規模復制實現的。

企業復制產品，個人復制IP，基因復制生命。

成功的復制，就是將某樣有價值的事物重復足夠多次，從而實現復利。

越厲害的復制，越是有指數效應，并且邊際成本遞減，還能形成網絡效應。

那么，復制什么呢？

動態 | CME比特幣持倉周報：調倉意愿持續下降，多空雙向持倉同步增長:10月19日，CFTC公布了最新一期的CME比特幣期貨周報（10月9日-10月15日）。該統計區間內價格的實際位移有限，市場參與者的調倉意愿仍然偏低。總持倉（未平倉總量）數量變化仍然非常有限，最新一期數據自3335張小幅回升至3444張，數字變化幅度非常有限。規模較大的經紀商持倉繼續回暖，多頭持倉自140張上漲至210張，而空頭持倉自138張進一步上漲至149張，多空雙向持倉的同步增長顯示上個月月底季度合約到期導致的減倉幅度已經基本得到了有效填補，經紀商對于比特幣后市仍然持相對樂觀態度。[2019/10/21]

在指數運算里，復制的是底數。例如，2的18次方是262144，其中底數是2，指數是18。

回到創業。

眾所周知的精益創業，其核心思想是，先在市場中投入一個極簡的原型產品，然后通過不斷的學習和有價值的用戶反饋，對產品進行快速迭代優化，以期適應市場。

精益創業的三個主要工具是：“最小可用品”、“客戶反饋”、“快速迭代”。

在大規模復制之前，創業者必須以最小的成本和有效的方式驗證產品是否符合用戶需求，在最短時間里找到有價值的認知。

快速地去蒙，聰明地去試錯，就像貝葉斯身后亂扔的球，以及過玻璃橋的大膽一躍。

這個有價值的認知，就是指數運算和對數運算中的底數。

創業的第一階段，從0到0.1或者從0到1，像是一個對數運算；

在經過驗證和迭代后，再實現爆發式增長。像是一個指數運算。

阿里云總裁認為技術只有兩個核心價值：

第一、對于驗證成功或接近成熟的業務，快速規模化，實現指數增長。

比如從1-10用了10天，那你從10-100應該只用兩天或一天。

第二、要幫業務團隊快速試錯。

讓產品快速上線，別在乎什么架構，有反饋才知道這個業務行不行，能不能活下來。

所以，創業的過程，交織著對數運算和指數運算。我們需要從兩頭分別輸入數字，往返測試，以求發現內核，然后進行大規模復制。

一頭計算作為復制內核的底數，一頭計算指數增長的規模。

我在《人生算法》里，將此拓展到個人的演化：

上半場，是一個切割鉆石的過程，目的就是為了不斷找到真正屬于你自己的最小的那個內核。

下半場，就是如何通過復制，令最小的內核最大化。

為什么要用“最小內核”來做指數運算的底數？

復利增長的關鍵是復制的連續性和穩定性，物理意義上去掉多余的部位，信息意義上去除噪音，能夠令最小內核的復制更可持續。

這個過程，總是伴隨著打破和重建。新晉導演章子怡認為，導演就是一個“打破瓶子”的過程：“你得把瓶子打碎了，鉆出來透口氣，再鉆進另一個瓶子里。”

尼采錯了，并非“那些殺不死你的，終將使你變得更強大”，而是你的強大需要通過殺死“不夠強大”而呈現出來。

正如演化算法的三部曲：變異，選擇，復制。

變異是某個認知，這個認知以某個最小化產品的形式被放在具體環境里，通過與環境的雙向選擇而不斷迭代，一旦其生存模式被驗證，就大規模復制。

一個人，或者一個機構，其成功的最大秘密是：找到可大規模復制的“大概率事件“。

log10(10000000)

事實上，馬斯克總是提及的第一性原理，也包含了類似的雙向推導。

先前，人們對“第一性原理”的理解主要是：

聲音 | 圣盈信將運用區塊鏈等技術助力金融業務及科技業務雙向發展:據證券時報報道，近日圣盈信金服集團董事長林建欣表示，現階段圣盈信在金融科技領域已擁有人工智能技術、大數據應用、區塊鏈應用、智能投研等多方面的技術儲備。依托這些技術，金融科技逐漸成為圣盈信傳統金融服務的高效催化劑及科技業務的發展起點，從而助力集團金融業務及科技業務的雙向發展。[2018/7/18]

把一些事情歸結為最基本的原則，尤其是物理定律，少一點兒類比，少一點兒夾層解釋。

但其實不止于此。

馬斯克說，另一個方法是：

在極限中思考問題。

如果你在思考一件事情的同時，把它擴展到一個非常大的范疇或一個非常小的范疇，事情會發生什么變化？

舉個例子，不管是造電動車還是火箭，假如零件太貴，成本太高，你就可以想：

如果每年的產量是一百萬臺呢？那還貴嗎？

如果一年一百萬臺還是很貴，那么數量就不是你的東西貴的原因，根本問題出在設計上。

這樣一來必須改變設計，改變零部件，從根本解決價格問題。

這個，是從規模極限去推導。

然后，倒過來，從基本單元的極限去推導，一直到原子層面。

例如生產火箭，一直拆解到初始的資源和原料：

如果你看一下火箭的原材料，你會發現原料有鋁、鋼、鈦合金、特種合金、銅等；

每個部件的組成元素的重量是多少，原材料價值是多少？

在不改變原材料的情況下，以上幾個問題為火箭的成本設定了漸近極限。

更進一步，把原子排列成最終的形狀，這將是你產品的最低成本。

在馬斯克看來，產品的制造成本漸進式地接近其原材料價值。

所以，關于產品的第一性原理是：

嘗試想象完美產品或技術，不管它是什么。然后思考：原子怎樣才能完美地排列？進而找出如何獲得這種形狀的物品。

但是，大多數時候，人們停留在“夾層”。從觀念上固守已有的東西，傾向于使用他們熟悉的工具和方法。

馬斯克的思考方式是，通過雙向推導：

我們一方面可以去發現規模效應下的完美產品；

一方面去創造工具、方法，找尋材料，從原子層面構建基本單元。

從因到果，再從果到因，雙向推導至極限，會創造出驚人的奇跡。

log10(100000000)

在《魷魚游戲》中的第五關“跳玻璃橋”，一個人向前跳，不管他踩中了鋼化玻璃，還是不幸踩碎普通玻璃，都為團隊提供了信息。

這種信息，是通過消除不確定性來實現的。

就信息本身而言，“正確”或者“錯誤”，是等價的。不同的是，“正確”的人有機會再去踩下一關的玻璃。

那么，該如何度量信息呢？

香農引入了“比特”的概念。

比特來自二進制，香農認為可能擁有的最簡單的信源，就是拋硬幣，正或反，是或否，1或0，這是可能存在的最基本的信息。

就像信息的原子。

比特是在兩個等概率的可能性之中進行選擇后所產生的信息量。所以“一臺擁有兩種穩定狀態的設備……能夠存儲1比特信息”。

回到開始的猜鉆石游戲，你需要多少信息？

在左右抽屜里二選一，對應1比特；再在黑白盒子里二選一，對應1比特；

所以你總共需要2比特，以實現在四個盒子里選出一個。

玻璃橋游戲里，總變化高達262144種可能性，但因為這是18個串聯在一起的二選一，我們算一下需要多少信息：

也就是計算262144以2為底的對數：log2262144=18，相當于2的18次方的逆運算。

為什么計算對數？

因為：采用概率分布的對數作為信息的量度具有可加性。

由于求對數，所以有一種逆向的指數效應。其所產生的加速效應，我稱之為逆向復利。

過玻璃橋的變化雖然很多，但信息只有18比特。

那么，每跳一個人，不管是否掉下去，就獲得了1比特。

當然，如果沒掉下去，就又多了一次下一輪的測試機會。

由此，每跳一次，就獲得了一個信息，也就消除了一部分不確定性。教科書對此的描述是：

香農將熱力學的熵，引入到信息論，因此它又被稱為香農熵，或信息熵。

在信息論里面，熵是對不確定性的測量。

在信息世界，熵越高，則能傳輸越多的信息，熵越低，則意味著傳輸的信息越少。其公式如下：

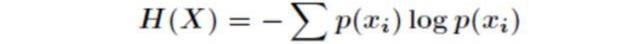
其中p代表隨機事件X為xi的概率。

還是以扔硬幣為例。

扔一次硬幣，出現正面的概率是p1=0.5,出現反面的概率也是p2=0.5。

所以，根據公式計算：

H=-(0.5log2(0.5)+0.5log2(0.5))=1比特

但是，如果這枚硬幣被做了手腳，出現正面的概率是0.7,反面是0.3。那么“扔一次這個硬幣”這個事件的信息熵是多少呢？計算如下：

H=-(0.7log2(0.7)+0.3log2(0.3))=0.88比特

假如你去玩拋硬幣的游戲，而且你知道有一桌的硬幣做了手腳，正面概率是70%，那么你一定會選這一桌，并且每次都押正面，因為其信息熵更低，這意味著該“不確定性”比公平的硬幣降低了。

在《魷魚游戲》里，那位玻璃廠的老師傅，就是靠自己的專業，降低了自己每一次蒙的行為的信息熵，就像上面那個做了手腳的硬幣。

因此，他消除不確定性的“能力”更強。

log10(1000000000)

再說回復利的主題。

復利的基本公式，是一個指數運算。

復利算起來很簡單，實現很難，原因見《復利的謊言》：

真相1、世界被隨機性主宰；

真相2、連續性很難實現；

真相3、現實是不均勻的；

真相4、回報是不對稱的；

真相5、籌碼是有限的。

用復利公式來描述以上幾點就是：

1、利率r與期數n都是說不準的；

2、比較好的回報r，期數n總是不長久；

3、利率r總是起起伏伏，時好時壞；

4、現值PV大，終值FV未必大；

5、以總值論，本金太小。以比例論，本金撐不到賺錢的時刻。

那么，復利公式還有用嗎？

在充滿不確定性的現實世界，用概率來描述一個事件，是理性且智慧的。

復利公式也不例外。

確定性下的復利公式是：

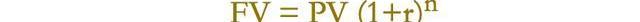
但是，現實世界的回報r并不確定，那么我們用概率來描述。

舉例：若一投資有60%的獲勝率，而投資者在贏得賭局時，可獲得一賠一的賠率。為了避免爆掉，所以下注者每次會控制下注比例，假設是x，那么連續下注n次，期望值計算是：

f(x)=(1+x)^(n0.6)(1-x)^(n0.4)

如上，這其實是一個概率世界的復利公式。

首先，這里仍然有一個重要前提：期望值為正。否則就是賭博。

這時，我們會發現，下注比例x太小，賺不到錢；x太大，可能會爆掉，以致無法實現遍歷性而“享用”正期望值。

有沒有一個方法，可以控制x的數值，就像用開關控制水量一下，調節每次下注的比例，在確保不會爆倉的前提下實現收益最大化？

轉化為數學問題，就是求上面f(x)的極大值。

當年索普向香農請教期望值優勢下的下注比例問題，香農向他推薦了自己同事凱利的一個公式。

與索普自己的信息熵公式有點兒像，凱利公式是對概率世界的復利公式取對數，然后求極值。

凱利公式的目標是：最大化資產的增長率，也即最大化對數資產的期望值。

設開始時的資產是1，每次下注的比例為f，有p的概率會以b的賠率贏錢，資產的對數期望值計算如下：

要找到最大化這個期望值f，只需E對f的導數值為零：

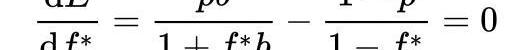
求解上述方程，得出凱利公式：

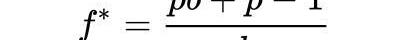
用圖形，更容易看出凱利公式的工作原理：

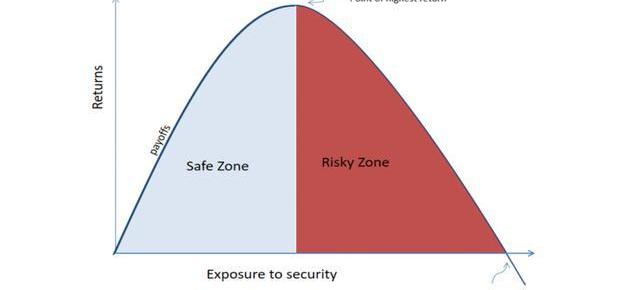
橫坐標是下注比例，縱坐標是回報。下注小，安全但回報低；下注大，極可能回報也不高風險卻很大。

凱利公式幫助我們找到圖中的峰頂，對應的就是最佳下注比例。

人的一生，是由很多個下注串起來的。雖然不像過玻璃橋那么非死即活，但一樣充滿了巨大的不確定性。

每次做決策時，計算一下輸贏的概率，算一下回報，并且隨時提醒自己控制好下注的水龍頭，千萬別Allin。

凱利公式的工作原理圖最上方的那個點，也許是我們想在人生中找尋的位置：活下來，活好。

log10(10000000000)

如上所述，對數與復利式的增長有關。

假設我們往銀行存1個億，銀行的年息是100%，如果每年產生一次，那我們可以知道一年到頭你的賬戶總額是：

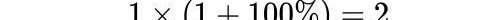
但是如果我們換成一個月產生一次利息，然后你又把每個月的利息重新存入本金，那你一年到頭的賬戶總額是：

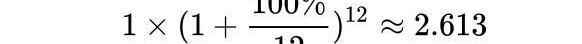
進一步，我們換成一個天產生一次利息，然后你把每天的利息重新存入本金，那你一年到頭的賬戶總額是：

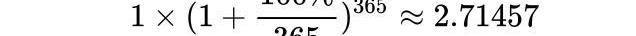
假設銀行愿意每秒付利息，你也每秒取出利息再存入，利滾利會不會漲上天呢？

并不會，你的銀行余額是2.7182817813元。

所以，1元錢存1年，在年利率100%情況下，無論怎么利滾利，其余額總有一個無法突破的天花板，這個天花板就是e≈2.71828…。

e，作為數學常數，是自然對數函數的底數，亦稱自然常數、自然底數，或是歐拉數。

在谷歌2004年的首次公開募股，集資額不是通常的整數，而是$2,718,281,828，正是來自e。其2005年的一次公開募股中，集資額是$14,159,265，與圓周率有關。

e和π，的確是兩個最神奇的數字了。

e的本質，是自然增長的極限。

e在自然界無處不在，最有名的是等角螺線，又叫對數螺線或生長螺線。

例如：

還有：

昆蟲以等角螺線的方式接近光源；

蜘蛛網的構造與等角螺線相似；

旋渦星系的旋臂差不多是等角螺線。銀河系的四大旋臂的傾斜度約為12°；

低氣壓(熱帶氣旋、溫帶氣旋等)的外觀像等角螺線。

雅各布·伯努利格外喜歡等角螺線。他發現了等角螺線經過各種適當的變換之后仍是等角螺線，并對此十分驚嘆和欣賞。

放大和縮小后的對數螺線，和原圖形相似。

還有旋轉的自相似性：旋轉后的對數螺線，和原圖形相似。

于是，雅各布·伯努利要求將等角螺線刻在自己的墓碑上，并附詞：

縱使改變，依然故我。

Tags：馬斯克哈耶克CEO馬斯克五大發明改變世界馬斯克什么星座馬斯克資產多少億美元哈耶克幣是什么幣CEO幣CEO價格

比特幣交易