零知識證明： Plookup算法介紹_以太坊

最近有空看了看Plookup的論文。針對對電路描述不友好的操作（比如bit操作），Plookup給出了新的思路和證明方式。給定某個操作的真值表示（lookup table），證明某個操作的輸入/輸出是在真值表中。這種方式，相對之前的bit計算約束方式，降低約束的個數，提高了電路效率。

Plookup的論文下載地址如下：

https://eprint.iacr.org/2020/315.pdf

基本思想

Plookup嘗試解決的問題是，給定兩個集合，證明某個集合的元素在另外一個集合中。給定兩個集合t和f，s是f排序后的結果。如果t中的元素最少在f中出現過一次。判別f中的元素是否包括在t中，只需要比較元素差的集合：

LayerZero Labs 與 Polyhedra Network 合作推出基于零知識證明的輕客戶端:5月31日消息，LayerZero Labs 宣布與 Polyhedra Network 達成戰略合作，共同推出基于零知識證明技術的輕客戶端，使得 LayerZero 的開發者只需要更新一個參數配置就可以使用 Polyhedra Network 開發的零知識證明協議。[2023/6/1 11:51:12]

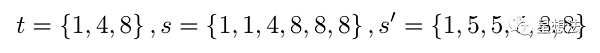
舉個例子，t是{1，4，8}的集合，元素的差異集合為{3, 4}，分別是4-1，8-4。如果s只有t中的元素組成，并且每個元素最少出現一次，例如{1，1，4，8，8，8}，元素的差異集合也為{3，4}。如果s中的元素并不完全是t中的元素，那即使在元素差異集合一樣的情況下，也不能說明s中元素在t的集合中。例如s為{1，5，5，5，8，8}，元素的差異集合也為{3，4}，分別是8-5，5-1。

零知識硬件初創公司Cysic完成600萬美元種子輪融資:金色財經報道，零知識 (ZK) 硬件初創公司 Cysic 完成了 600 萬美元的種子輪融資。該輪融資由 Polychain Capital 領投，其他投資者包括 Hashkey、SNZ Holding、ABCDE 和 Web3.com 基金會。[2023/2/17 12:13:48]

論文提出，可以引入一個隨機因子，將前后兩個元素相加的方法，確定兩個集合的依賴關系。

定義多項式

在基本思想的基礎上，論文在第三章定義了兩個多項式F和G：

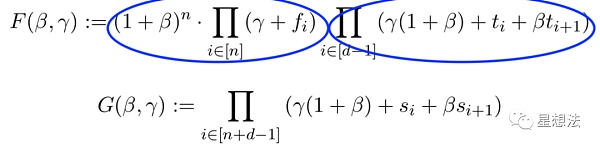
以太坊生態零知識協議Semaphore發布V2版本:7月7日消息，以太坊生態針對開發者的零知識協議 Semaphore 推出 V2 版本，更新內容包括不再需要擁有 EdDSA 私鑰，從而實現更簡單的電路（circuit）和更高效的零知識證明生成；用于身份承諾和 Merkle 樹的哈希函數從 MiMC 遷移到 Poseidon，將證明時間減半并提高了 Gas 效率；合約模塊化、三個新的 JavaScript 庫等。

Semaphore 最早由以太坊社區成員 Kobi Gurkan、Koh Wei Jie 和 Barry Whitehat 提出，在 2019 年發布 V1 版，可以讓以太坊用戶可以證明他們的群組成員身份，并在不透露原始身份的情況下發送諸如投票或支持的信號。Semaphore 不是面向用戶的應用程序，旨在為以太坊開發人員提供強大而簡單的工具，以使用私有憑據構建 DApp。[2022/7/7 1:57:35]

如果F和G相互對等，有且如下的條件成立：

f集合屬于t

s是(f，t)的并集，并且按照t中的元素排序

如果條件成立，可以推導出兩個多項式相等。F多項式可以看成是兩部分組成，分別是兩個連乘。后面的連乘可以看成是t中的元素連乘。前面的連乘，可以看成是f中元素的連乘。因為f中的元素屬于t，則f中的元素的連乘，可以想象成多個相同元素的連乘。反之，因為beta和gamma的隨機因子，也能從F和G對等條件推出滿足的兩個條件。具體的證明過程，可以查看論文的第三章。

在定義多項式的基礎上，問題可以轉化成兩個多項式相等。

Plookup協議

已知f和t，可以排序得到s。因為s由f和t合并而成，s可以由兩個函數h1和h2表示。關鍵在于第4步，定義了Z函數：

Z(g) = 1 - 初始為1

Z(x) 是兩種多項式表示的商

Z(g^(n+1)) = 1 - n+1元素的連乘，兩種多項式表達式相等

驗證者，除了查看Z函數外，額外還要查看h1/h2連續性。

論文進一步將協議推廣到更通用的情況，并給出了t中元素是連續情況下的優化協議。感興趣的小伙伴可以自行查看。

Plookup提出了一種明確輸入/輸出的情況下，如何證明某個函數的運算正確的協議。輸入輸出定義成lookup表，計算的輸入/結果只要在該lookup表中即表示運算正確。和Plonk采用同樣的思路，Plookup定義了問題的多項式表示，證明了Z函數的遞歸表示和邊界。

Tags：LOOKOKUPLO以太坊looks幣今天最新消息SOKUDO FINANCEPLOT幣以太坊交易時間

火必下載