如何利用門限簽名來生成隨機信標？_DEF

編者按：本文來自：以太坊愛好者，作者：ALEXANDERSKIDANOV，翻譯&校對:IANLIU&阿劍，Odaily星球日報經授權轉載。

回顧2015，DFinity項目提出了令整個社區都為之興奮的隨機信標方案——使用BLS門限簽名產生隨機輸出，同時保證輸出的無偏性及不可預測性。然而，時至2020年的今天，構建無偏且不可預測的隨機信標仍然困難重重，還在研究的項目少之又少。其實門限簽名只是構建隨機信標的可行方法之一，我們前面發表過一篇概覽文章，介紹其他可能的解決方法，其中包含本文要重點提到的一種。其他細節——隨機信標是什么？什么是無偏性及不可預測性？除了門限簽名還有什么方法——這些問題都能在上述概覽中得到解答。經過了多次設計迭代，我們最終提出類似DFinity的方案，這也是我們進一步深入理解隨機信標的大好契機。本文將以淺顯的形式，講述門限簽名生成隨機數的一系列協議。密碼學基礎知識

為了更好地了解本文中提到的隨機信標，我們需要掌握一些基礎密碼學知識。首先，我們必須區分兩個概念：1.在本文中以小寫字母表示標量，或者說普通常量；2.用大寫字母表示橢圓曲線上的點。我們不需要對橢圓曲線點了解得很透徹，只要掌握下面兩點：橢圓曲線點可以相加，也可以跟標量相乘，然后得到另一個橢圓曲線點。即使知道G和xG的值，也不可能計算出x的值。在本文中，我們還將用到k-1階多項式p(x)；關于p(x），你不用想太多，只要把它當成一個方程就好，而且：只要你知道在k個不同的x下p(x)的值，你就能推導出所有x的p(x)值。以此類推，對于同一個函數p(x)和基點G，如果你知道p(x)G代入k個不同的x值后的值，就可以推導出所有x所對應的p(x)G值。只要明白了有關橢圓曲線點的這些屬性，就能深度理解隨機信標的工作原理了。隨機信標

CFTC技術團隊正嘗試了解應如何處理DeFi:美國商品期貨交易委員會（CFTC）的技術咨詢委員會正在嘗試了解應如何處理DeFi。該委員會周一主持了一場演講，題為”DeFi的增長和監管挑戰”，演講者是法學教授Aaron Wright和律師Gary DeWaal。Wright總結了DeFi的優勢，即通過自動化多個相關流程，可以為更多的人提供成本更低的服務。此外，演講者提及DeFi具有潛在風險，如高技術準入壁壘等。對于“如果DeFi平臺非法運作，當局應該追究誰的責任”，DeWaal表示，這是一個難以逾越的法律障礙。次要責任可能會威脅到使用或參與DeFi協議的廣泛人群。（cointelegraph）[2020/12/15 15:12:05]

假設1：系統中有n個參與者，至少需要其中的k位才能產生隨機數。就算控制其中的k-1人，你也不能預知隨機信標的輸出結果、無法操縱結果。

假設2：現在有個k-1階多項式p(x)，參與者1知道p(1)的值、參與者2知道p(2)的值、……、參與者n知道p(n)的值；大家約好使用G作為橢圓曲線基點，所有參與者都知道p(x)G代入所有x的值。我們將p(i)視為參與者i的“私人份額”，而p(i)G是其“公開份額”要設計好的隨機信標，最困難的部分，就是要找到這么一個多項式，使得每個參與者都能知道自己的私人份額，但是無法知道他人的私人份額——這也被稱為分布式密鑰生成。DKG會放在下個章節討論，現在就先假設存在這么個多項式，而所有人都知道各自的私人份額。我們接著討論，如何使用這套假設在區塊鏈協議中產生一個隨機信標？假設網絡產生一個區塊，區塊哈希為h。現在參與者們想用h作為種子以生成隨機數，首先用約定好的函數，將h轉換為某條橢圓曲線上的一個點：H=scalarToPoint(h)對于參與者i來說，因為他知道p(i)和H，所以可以自行計算出H_i=p(i)H。對外公布H_i并不會導致參與者i的私人份額p(i)暴露，因此在每個區塊中都能重用同樣的私人份額，因此DKG只需要進行一次。根據前面提到的第三點特性，當至少有k位參與者公布他們各自的H_i=p(i)H之后，其他人就能知道代入任何一個x之后，H_x=p(x)H是什么。然后所有參與者都可以在自己本地計算H_0=p(0)H，并以這個結果的哈希值作為隨機信標的輸出；請注意，因為沒有參與者知道p(0)，所以唯一能得到p(0)H的方法就是對p(x)H進行內插法計算，要完成內插計算需要知道至少k個p(i)H的值。如果公布的人不足k位，則其他人無法推出p(0)H的值。

聲音 | 前FDIC主席：對Libra有些擔憂 不知道其如何利用獲得的資 金:據CCN消息，前聯邦存款保險公司（FDIC）主席Sheila Bair在接受CNBC采訪時對Libra提出了一些擔憂，“如果我給他們一些錢去買Libra，他們會用這些錢做什么？他們在白皮書中對此有點模糊……抵押品的實力是我會問的一個問題。”盡管Libra聲稱自己是未來的穩定幣，但尚不清楚Facebook將如何利用其外匯儲備管理投資。 Bair后來重申了她關于美聯儲支持的加密貨幣的想法，然而，這一想法并沒有實現。政府通常對新技術的吸收很慢，但如果成功的話，Libra可能會改變這一切。[2019/6/19]

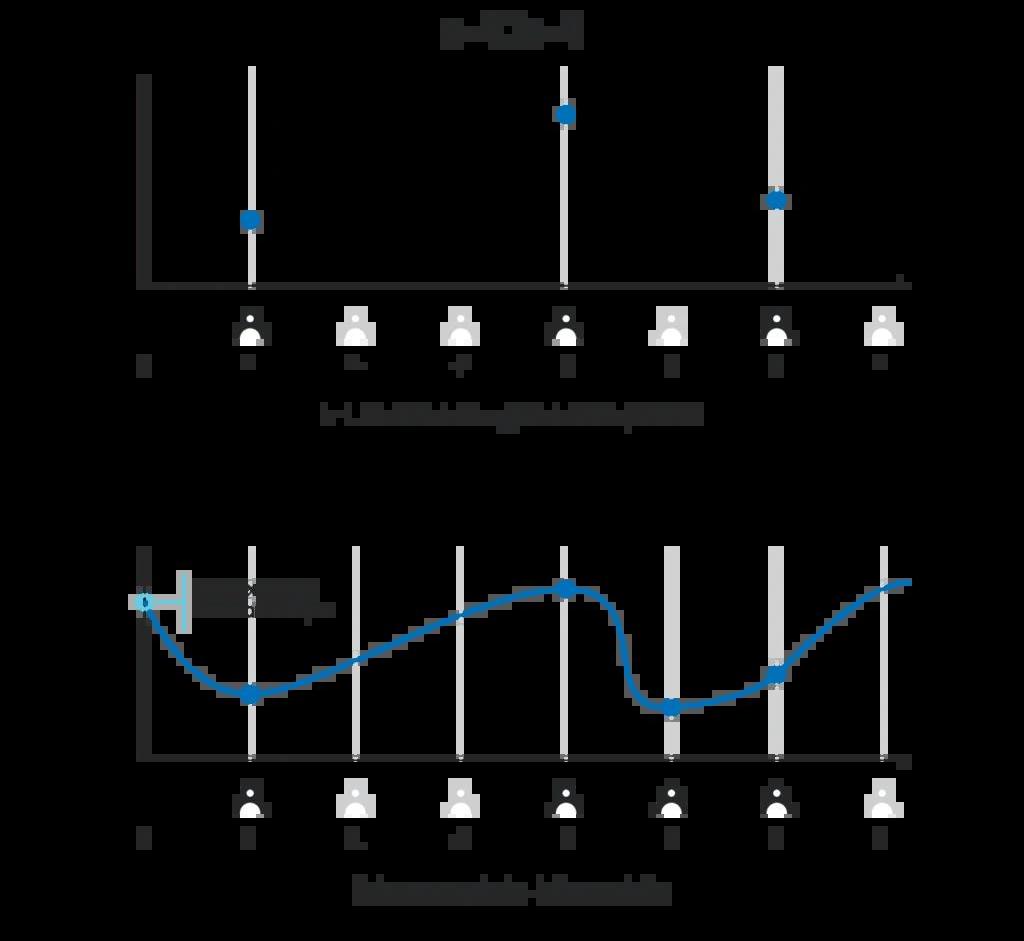
基于此技術構建的信標延續了這些我們所需的特性：如果攻擊者只掌控了少于k-1位參與者，則他無法操控隨機信標的輸出；其他k位參與者才能計算出最終輸出，他們的子集或其他更多的參與者，都能得出相同的輸出。我們還忽略了一件事。為了使用插值法計算p(0)H，必須保證參與者i所公開的H_i真的等于p(i)H。但是因為除了參與者i，其他參與者都不知道p(i)是什么，所以沒法直接驗證參與者i公布的H_i是否的確等于p(i)H；如果不要求為H_i附上密碼學證明，攻擊者可以直接聲稱某個H_i的值，而其他人沒有辦法辨別真偽。

聲音 | 救助兒童會Paul Ronalds：慈善機構領導者也應去了解區塊鏈等技術如何運作:根據Coincryptorama消息，救助兒童會首席執行官Paul Ronalds在關于區塊鏈對慈善事業的潛在影響的小組討論后表示，慈善機構對區塊鏈的使用還處于初期階段”，要在其潛力被夸大之前需要進行更多的討論和研究。慈善機構面臨的主要障礙之一是，當涉及區塊鏈這種存儲數據的方法時，行業領導者并不能很好理解，我們需要確保慈善機構領導者同樣參與、了解數字世界以及如何運作區塊鏈等技術，來幫助他們的做好慈善事業。[2018/9/3]

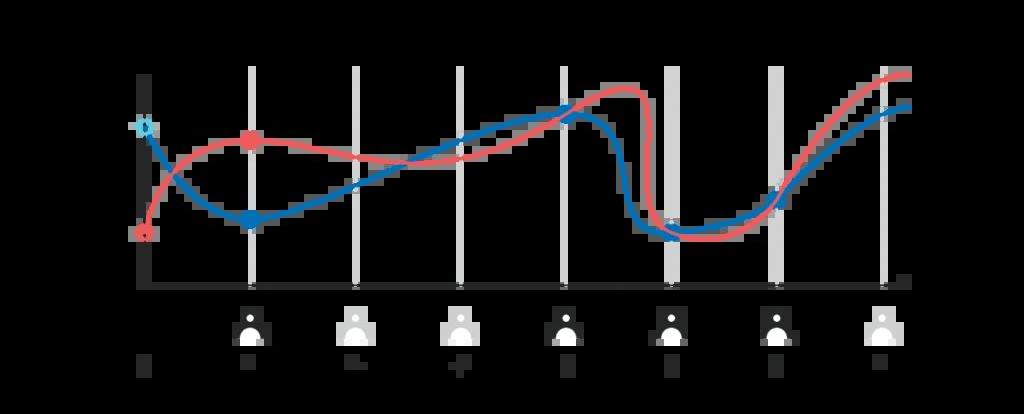
有至少兩種密碼學證明辦法，可以用來判別H_i的真偽。我們會在聊完DKG之后介紹。分布式密鑰生成

根據前面章節對隨機信標的介紹，我們需要n位參與者共同使用某個k-1階多項式p(x)，使得每個參與者i知道自己的p(i)，而其他人無法得知。下一步，需要所有參與者都知道：給定G時，所有的x所對應的p(x)g值。在本章節，我們假設每個人都有自己的私鑰x_i，而且其他人都知道x_i對應的公鑰X_i。那么運行DKG的一種方式如下：

韓國政府正在考慮如何兌現沒收得來的加密貨幣:韓國政府正在考慮如何兌現最近沒收所得來的加密貨幣。作為一起刑事案件罰款，政府沒收了網站運營商“安恩”(Ahn)的191.32333418個比特幣。韓國最高法院此前判定，加密貨幣是政府可以沒收的財產。最有可能的選擇是通過政府所有的拍賣平臺進行拍賣。[2018/6/10]

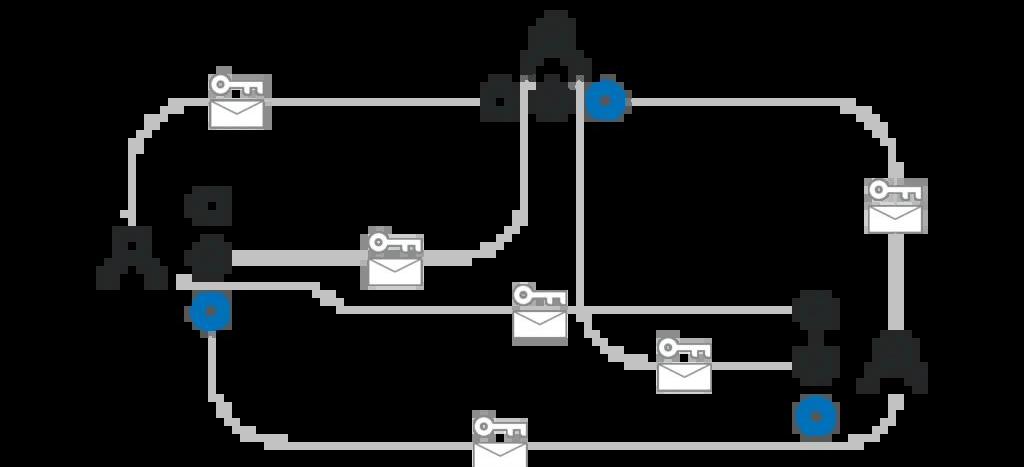
每個參與者i在本地運行k-1階多項式p_i(x)的計算。接著用公鑰X_j將每個p_i(j)加密，并發送給對應的參與者j。如此一來，只有參與者j能解密出p_i(j)；參與者i還要公布所有p_i(j)G，j∈1~k。所有參與者要對一個至少由k個多項式組成的集合達成共識。因為有些參與者可能掉線，所以他們不可能等到n個驗證者都作出如此承諾再進行下一步；只要至少k個驗證者都作出“收到至少k個這樣的多項式”的承諾之后，他們就可以使用某種形式的共識算法對他們所收到多項式的子集Z達成共識。所有參與者共同驗證加密的p_i(j)與公開的p_i(j)G是否對應，并從Z中移除不合格的多項式。對于集合Z中的每個多項式p_i(x)，每個參與者j自行計算p_i(j)的總和作為私人份額p(j)；同樣的，對于集合Z中的每個p_i(x)G，參與者可以計算p_i(x)G的總和作為公開份額p(x)G。

比特幣共識大會圓桌討論有關政府如何使用加密技術:今日比特幣共識大會召開，在有關政府如何使用加密技術的圓桌討論環節，德勤高級經理Wendy Henry表示，美國正著眼于能夠實現現代化的技術。這些技術例如區塊鏈技術，實際上可以作為連接的組織，人們必須弄清關于如何使用區塊鏈技術。linux基金會首席營銷官Jamie E. Smith表示，區塊鏈技術并非將房子燒毀一樣的革命，而是提供政府目前已經提供了的服務的更好版本。[2018/5/15]

因為p(x)是每個獨立的p_i(x)的總和，每個p_i(x)都是k-1階多項式，所以要觀察p(x)是否也是k-1階多項式。其次要注意，每個參與者j只知道p(j)的值，但不知道其他p(x)的值。實際上，為了知道p(x）的值，TA需要知道所有的p_i(x），只要至少一個被承諾多項式的值屬于未知，TA就不可能知道p(x)。上述步驟組成了完整的DKG過程。步驟1、2、4相對直觀，但第3步就比較復雜了。具體來解釋第三步——我們需要找個方法，證明每個加密的p_i(j)與公開的p_i(j)G存在對應關系。如果沒有這種驗證，攻擊者i可以向參與者j胡亂發送消息，而不是發送正確的加密p_i(j)，導致參與者j無法進一步計算自己的私人份額。雖然有辦法可以制作出加密份額的形式正確性密碼學證明。但是，這樣的證明數據過大，并且要向全網公布這樣的證明，時間復雜度可能高達O(nk)，證明的size是嚴重的瓶頸。在NEAR協議中，我們不去證明p_i(j)與公開的p_i(j)G的關系，而是在DKG過程中給予每個參與者充分的時間，去證明“他們收到的p_i(j)與公開廣播的p_i(j)G對不上”。協議中假設每個參與者在窗口期內至少會上線一次，而他們提交的挑戰就能進入區塊鏈。對于區塊生產者來說，這兩個假設都很合理，因為要做區塊生產者，一般來說在整個epoch中都要在線；如果大多數區塊生產者密謀不接收這條消息，其實整個系統就已經不安全，攻擊者其實有更好的方式攻擊整個系統。

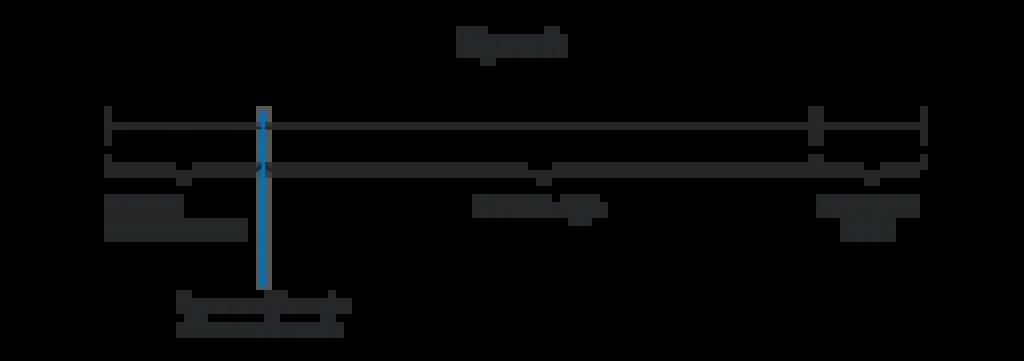
假如某個區塊生產者收到無效的公開份額，而且沒有及時在DKG過程中提出挑戰，則該礦工也無法在該時段中參與隨機數生成。請注意，只要其他k個誠實的參與者都能正確計算出份額，協議仍將正常運作。證明

還剩下最后一個問題：我們如何以不透露p(i)為前提，證明自己公布的H_i等于p(i)H？回想一下，每個參與者都知道H、G、p(i)G的值。在給定p(i)G和G的情況下回推p(i)的運算被稱為離散對數問題，又簡稱為dlog。那么每個參與者想做的都是：既能向他人證明dlog(p(i)G,G)=dlog(H_i,H)，又不會透露p(i)。的確存在這么一種方法構建上述證明，其中之一就是——Schnorr協議；通過Schnorr協議，參與者能在發布H_i時附上H_i的正確性證明。回想一下，隨機信標連的輸出是H_0的內插值。對于沒有參與生成隨機信標輸出的人來說，除了H_0，還需要哪些信息來驗證這個值的正確性？因為每個人都能自行在本地計算中加入G_0，所以只要證明dlog(G_0,G)=dlog(H_0,H)就行了。但因為信標的特性，我們無法得知p(0)，也就無法通過Schnorr協議生成這樣的證明。所以如果你要向其他人證明H_0的正確性，就必須保留所有H_i的值及其相應的證明。不過，好消息是，如果有些計算類似于橢圓曲線點乘法，則只需驗證H_0×G=G_0×H即可證明H_0的計算正確無誤。如果所選的橢圓曲線支持橢圓曲線配對運算，則這種證明是可行的。在這種情況下，任何知道G，H和G_0的人都可以核實H_0；而且H_0也可視作一個集體的多重簽名，證明區塊n的正確性得到至少k位參與者的檢查認證。目前我們還未在NEAR中使用橢圓曲線配對運算，但未來我們可能會使用，然后利用上文討論的小技巧取代我們當前使用的單一簽名方法。另一方面，DFinity使用BLS簽名，可以利用配對運算來實現上述簽名。

Tags：區塊鏈DEFDEFIEFI區塊鏈技術最早應用于defy幣是真是假DeFi ForgeRio DeFi

幣安交易所app下載