Paradigm解讀新型衍生品「乘方永續合約」_PARK

線性函數與凸函數

目前所有的金融衍生品，不論其產品的具體結構設計如何變化，其核心都是要構造一個底層資產價格對衍生品價格的映射函數。在這個思路下，主流衍生品可以按照其映射函數的類型分為以下兩類：

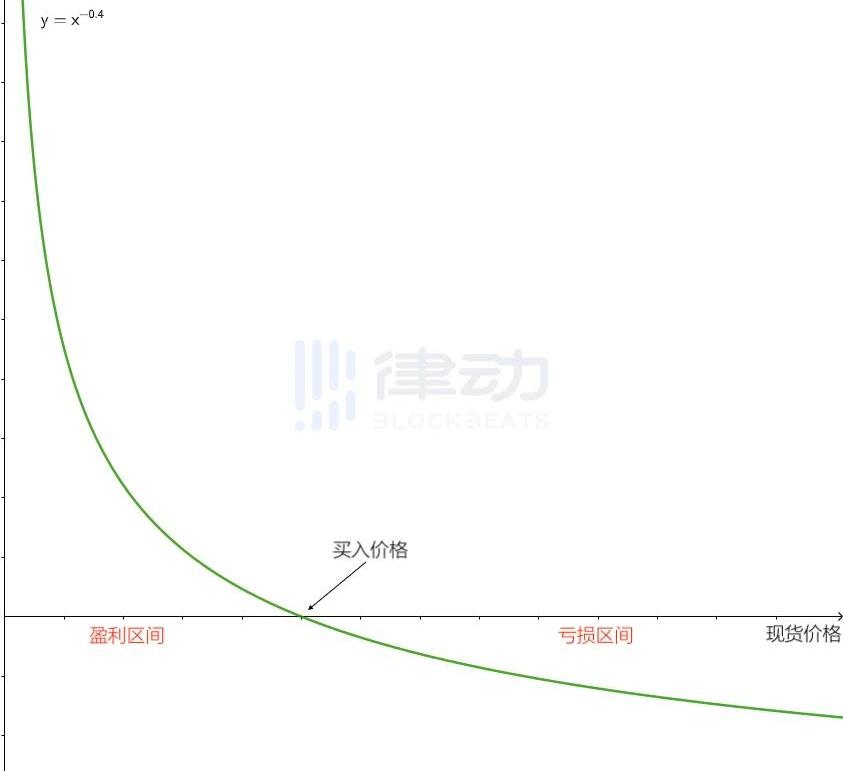
第一類為線性函數類衍生品，其衍生品的價格會根據現貨價格的變動而線性變化，對應的產品就是傳統金融中的期貨合約，在此不做過多介紹。而第二類為凸函數類型衍生品。其典型特征為衍生品的價格與現貨價格的變動成非線性關系，比如在現貨價格上漲時衍生品價格上漲的幅度更大。而在數學上，凸函數也有明確的幾何特征，在不追求嚴謹數學定義的前提下，凸函數可以被簡單的理解為一個函數曲線向上或向下彎曲的函數。下圖是隨機生成的一條函數圖像向下彎曲的凸函數，如果我們使用這個函數構建一個衍生品，其中x軸代表現貨價格，y軸代表衍生品的價格。那么這個衍生品的持有者，就會獲得一種不對稱的風險與收益，當現貨價格上漲時，衍生品持有者的收益增長幅度更大，而當現貨價格下跌時，衍生品持有者虧損的速度卻會更小。

ParaSwap 計劃全面啟動質押者 Gas 退款:3月16日消息，DEX 聚合器 ParaSwap 的 PSP-IPΔ13 相關投票結束，質押者 Gas 退款提案已擬定。官方團隊并計劃于北京時間 3 月 21 日 20：00 點開始全面啟動 Gas 退款，屆時將分配 3000 萬枚 PSP。[2022/3/16 13:59:26]

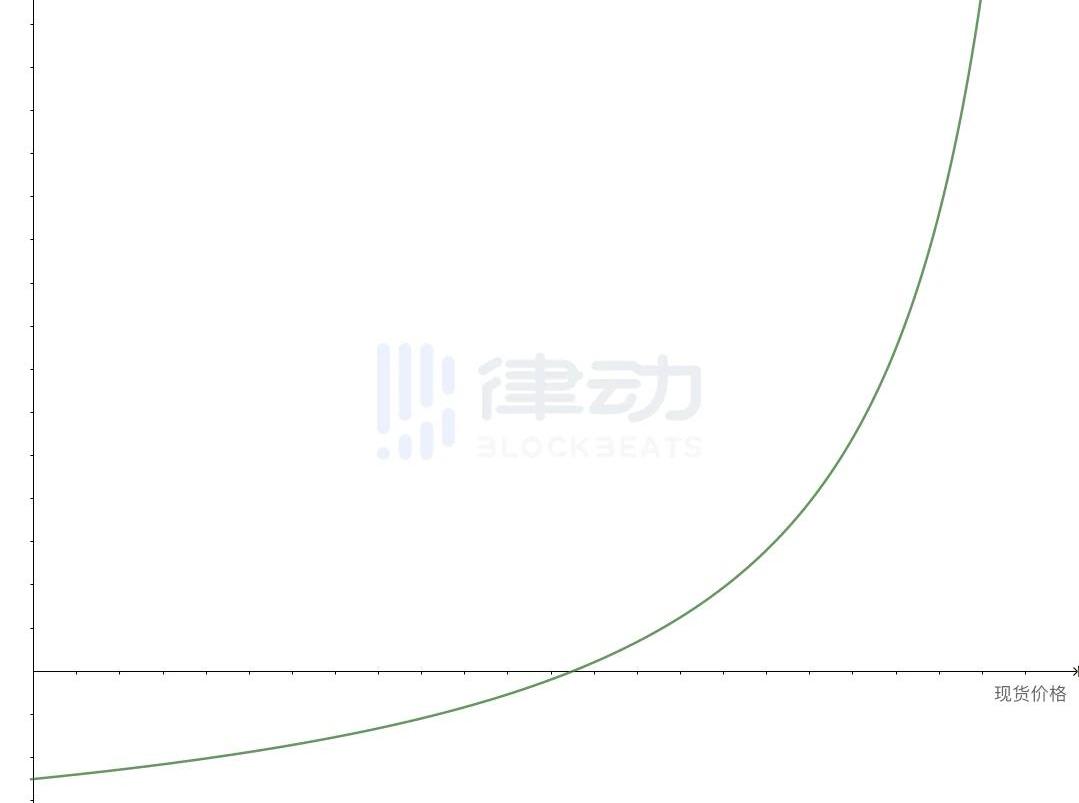
讀者可能已經發現，這種風險收益模式就很類似看漲期權的盈虧模型。因此所有期權類衍生品的核心特征，也可以概括為風險與收益的不對稱性，這種屬性也常被稱為凸性或Gamma值。這種由凸函數帶來的不對稱的風險與收益組合，為投資者提供了一種十分理想的投資組合風險管理工具。因此具有凸性的金融產品，在傳統金融市場中一直占據著很大的市場份額，常被專業投資機構用來調整投資組合的風險敞口，或構建更為復雜的衍生產品。然而美中不足的是，傳統的期權類產品受制于買權、賣權交易的具體實現形式，因此總是難以徹底擺脫產品會不斷到期以及需要行權的缺點。雖然業內一直在進行相關的探索，嘗試構建一種沒有到期日的「永續期權」產品，但效果卻一直不甚理想。由Paradigm最新論文提出的「乘方永續合約」，便是對這一經典命題的最新回復。它嘗試結合已經成功驗證過的永續合約產品結構，并通過將其核心函數由線性函數調整為凸函數，試圖解決曾經的「永續期權」一直沒能真正解決的問題，那就是：構造一個不會到期也不需要行權，同時具有凸性的衍生品類別。對傳統衍生品的重構

DeFi保險市場CoverCompared將于1月19日發布主網DApp:1月16日消息，DeFi保險市場CoverCompared（原PolkaCover）發推稱，將于1月19日在主網發布其DApp。[2022/1/16 8:52:58]

我們參照上文的思路，利用永續合約經典的資金費模式，分別對兩種映射函數進行產品重構，便會得到兩種新的衍生品形式。

從上表中可以看出，所謂乘方永續合約，就是利用了永續合約的資金費機制，構建了與期權風險模式類似的不對稱風險敞口的產品。這種結合了資金費機制以及期權類風險敞口的「乘方永續合約」，較傳統期權產品具有了以下明顯優勢：1.產品結構更為純粹，不再有交割期、行權價等額外環節，買賣雙方可以單純交易具有凸性的風險敞口；2.從根本上解決了同一交易對的流動性割裂問題，交易效率大大提高；3.底層邏輯更簡單，方便在計算資源有限的公鏈上進行產品實現；4.統一了凸函數類與線性函數類衍生產品的底層函數。從上表中可以看出，y=x其實就是

Arweave與Parity Tech合作發起建立橋接的賞金計劃:金色財經報道，去中心化存儲協議Arweave宣布與波卡（Polkadot）開發公司Parity Tech合作，將共同發起一項賞金計劃，以建立從波卡及其平行鏈到Arweave網絡的數據檔案橋接。黑客馬拉松將于1月28日至2月25日舉行。[2021/1/30 14:23:00]

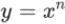
在n=1時的特殊形式。因此一個衍生品協議，可以僅依靠同一個底層映射函數公式，便能模擬期貨與期權兩類不同的風險敞口；乘方永續合約如何體現期權交易的四種風險敞口

我們知道，傳統的期權類產品包含四種不同的風險敞口，他們分別是：買入看漲期權、賣出看漲期權、買入看跌期權和賣出看跌期權。他們的定價函數圖像如下：

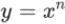
Flare Network已完成Spark代幣的快照:據官方消息，Flare Network已于北京時間12月12日8時（XRP Ledger區塊高度60,155,580）完成針對XRP持有人空投的Spark（FLR）代幣快照，此前消息，Flare Network的Spark代幣總量1000億枚，單個XRP持有人預期總共收到的Spark數量可按公式計算。在網絡啟動時，每個帳戶將獲得他們符合條件的Spark總數的15%，余下將在25到34個月分配。[2020/12/12 14:59:18]

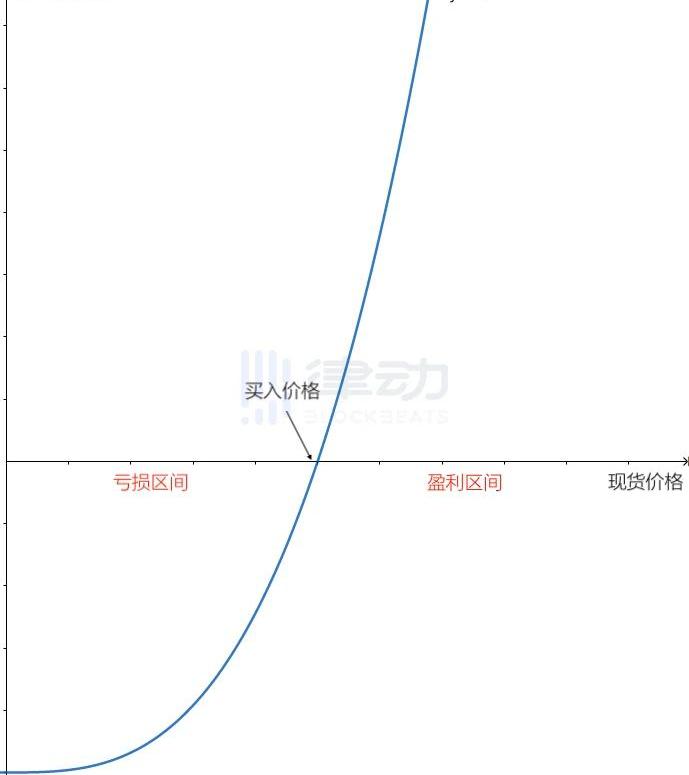
中n的取值，嘗試構造與傳統期權函數相似的四種函數圖像。買入看漲期權當n>1時，則函數圖像會向下突出。乘方永續合約的多方在現貨價格上漲時收益增幅更快，現貨價格下跌時虧損速度較慢，可以較好的模擬看漲期權的風險敞口。

動態 | PARSIQ監視平臺已支持監視比特幣網絡:PARSIQ監視平臺已支持監視比特幣網絡，其用戶現可跟蹤比特幣網絡數據和分析比特幣網絡活動。（CryptoNinjas）[2020/1/7]

賣出看漲期權在上圖的函數中，如果交易者不選擇做多而是做空，則其盈虧函數則與上圖正好相反。也就是按照x軸對函數圖像進行翻轉。其持有者的收益特征也與賣出看漲期權類似，在價格下跌時收益增幅較慢，而在價格上漲時虧損可以快速增長，對應傳統期權類的賣出看漲期權。買入看跌期權如何通過乘方永續合約構建看跌期權，似乎在論文中并沒有提及。于是我們嘗試將n取為小于零的負值，便會得到一條現貨價格上漲時虧損緩慢增加，而下跌時收益快速增長的函數圖像。這條曲線的多頭持有人的盈虧模型，與傳統看跌期權的收益模式非常類似，只是函數曲線與x軸不再相交，于是形成了在虧損時收益可以無限增長的特性。

賣出看跌期權同理，在上圖函數中的空方，持有的是原函數對x軸的倒影函數。其在價格上漲時收益增速較慢，而在價格下跌時虧損會快速擴大，對應了賣出看跌期權的風險收益模型。

乘方永續合約的定價

文章的最后，我們需要簡單討論一下乘方永續合約的定價問題。期權之所以需要定價，與其凸函數的性質緊密相關。上文提到，凸函數的持有方獲得了一種收益與風險不匹配的風險敞口。于是想要購買潛在收益大于潛在風險頭寸的一方，只有向其對手方支付一定的溢價，才能緩解交易的不公平性并使得交易成交。這種溢價，在傳統期權中表現為期權的購買價格。而在乘方永續合約中，則會表現為多方向空方定期支付的資金費。這種由多方定期支付資金費的形式，相當于多方在一定期限內，向空方「租用」了這種不對稱的風險敞口。且其租用時間可以自由調整，不再受到傳統期權到期日的限制。同時，也由于這種溢價的存在，使得函數的成交價格會高于函數圖像本身，這也是論文中的函數圖像會同時具有兩條曲線的原因。下圖中的藍線是

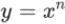
函數圖像本身，黃線是考慮溢價之后的理論成交價格，而黃線高于藍線的部分，就是乘方永續合約的多方向空方支付的風險溢價。

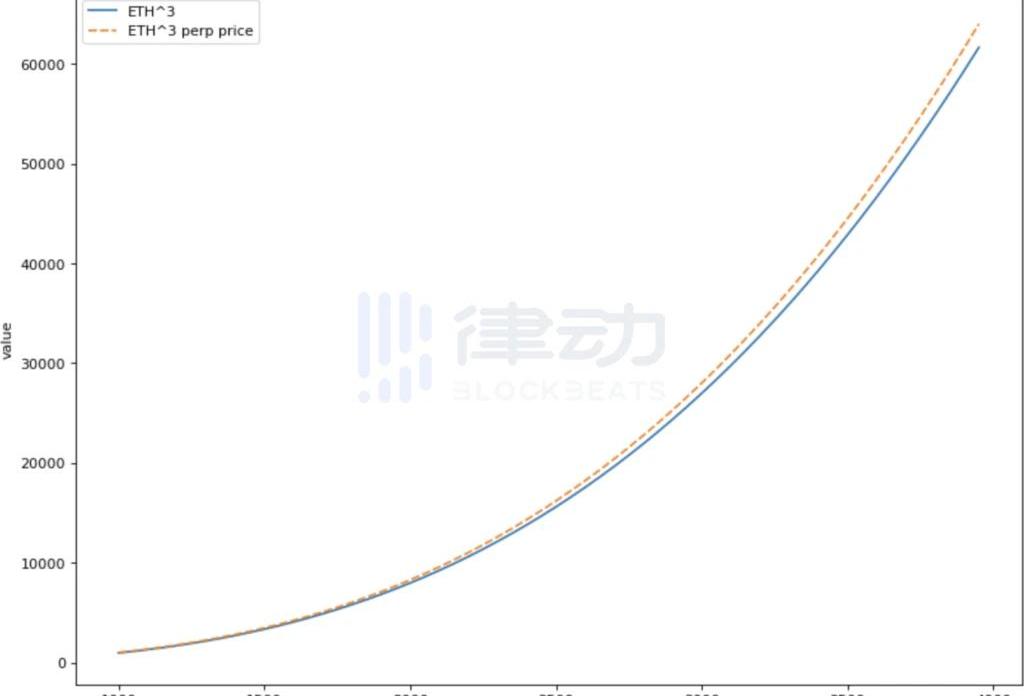
那么下一個問題自然是，黃線應該高于藍線多少才屬于合理的溢價？論文中用復雜的公式詳細討論了這個問題，而在這里讀者可以暫時不去理解復雜的數學公式，只要知道這個溢價的大小會受哪些因素的影響就可以了。與傳統的期權產品一樣，乘方永續合約的價格，也就是上文中的溢價，會受到底層資產的波動性、無風險利率的影響。底層資產的波動性越高，乘方永續合約買方支付的溢價就越高，也就是黃線與藍線的距離越大。此外，代表曲線彎曲程度的n的絕對值越大，代表產品收益與風險的不均衡程度越多，也會使得溢價金額變高。本文僅基于基本的理論推導，嘗試對乘方永續合約可能的應用場景進行討論，如有不足之處還請專業人士批評指正。我個人對這項創新的第一時間感受是，如果這種模型真的能夠落地并被產品化，且沒有在應用階段被證偽，那么其有可能是一個與現貨AMM交易機制同等重要的創新。非常期待能有專業團隊將乘方永續合約的設想產品化，并使其能夠在真實的市場環境中接受考驗。

Tags：PARPARKSPASPARKMemoparkautoparkspacepi幣價格SPARKS

以太坊交易