自動做市商（AMM）算法的數學原理及其未來發展_CUR

本文總共分為中篇闡述自動做市商算法、現狀及未來迭代的思考，本文為中篇。下篇請點擊

目錄

7.? Curve的StableSwap和交易公式

8.? Curve V2 的動態權重、可定制的價格錨定和平滑的價格過渡

9.? Curve V2 在 2 代幣池中的做市商函數

10. 與 CPMM 和 StableSwap 相比，Curve V2 的價格函數

11. 價格重錨過程：Xcp 標準、EMA 價格預言機、相對價格變化步長 s

12. Curve V2的動態交易手續費

13. DEX聚合器：Balancer SOR算法的通用解決方案

14. Pivot 算法：解決無常損失問題的一種嘗試

15. 單邊流動性解決方案

Curve的StableSwap和交易公式：

Curve 將 恒定加和做市商 (CSMM) 和 恒定乘積做市商(CPMM) 合并在一起，以實現更低的價格滑點。我們可以把這個算法看作是向 Uniswap/Balancer 模型添加一個固定價格部分，使最終的做市函數錨定于一個價格。

Curve1? V1，被稱為 StableSwap，設計了用于穩定幣交易的算法。它將 CSMM 與權重相乘并加上CPMM：

Curve1? V1

StableSwap — efficient mechanism for Stablecoin liquidity

https://curve.fi/files/stableswap-paper.pdf

首先我們考慮一個特殊情況，即流動性池中每種代幣的數量是相同的。很容易證明在平衡點處時這個方程成立（χ 是權重，與D??1 相乘以使 CSMM 和 CPMM 具有相同的數量級）。但是，當流動性池失衡時，如果 χ 是一個常數，則該等式將不再成立。因此，我們需要將 χ 變量化。Curve V1 選擇了一種 χ 的函數形式，使它在流動性池極端不平衡時變為零，這意味著該方程由 CPMM 主導。在平衡點下，χ 等于 A。A 是一個常數，通過模擬歷史數據進行優化。代入 χ 給了我們一個始終成立的方程。

自動做市商BurgerSwap發布補償計劃:官方消息，BSC鏈上首個自動做市商BurgerSwap發布補償計劃，在區塊高度7781159（5月27日06:54:46 PM之前，UTC時間），持有遭受攻擊的BURGER LP將有資格獲得補償。

此前消息，BurgerSwap更新閃電貸細節，共被盜走4400枚WBNB、140萬枚USDT等代幣。已修復Bug并重新開放兌換和流動性，隨后公布補償計劃。[2021/5/31 22:58:10]

接下來，讓我們推導出 StableSwap 如何實際計算交易結果。根據當前池中的代幣數量，我們可以計算出 D。例如，如果我們想換出代幣 j，我們可以將 x? 分離開來并求解 x? 的方程：

該方程可以簡化為二次形式。可悲的是，現在鏈上Vyper語言里沒有可以解二次方程的數學庫。因此，StableSwap 使用了牛頓法來求解 x?。迭代公式每次迭代都將其精度加倍。因此，可以在設定的gas上限內計算可接受的 x?。最后，交換前后 x? 之間的差值將是購買的代幣 j 的數量。

牛頓法

它是一種在實數域和復數域上近似求解方程的方法

https://en.wikipedia.org/wiki/Newton%27s_method

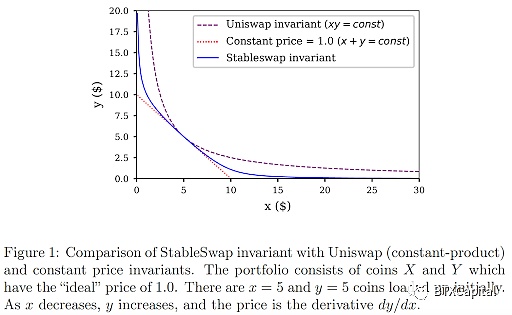
From StableSwap whitepaper

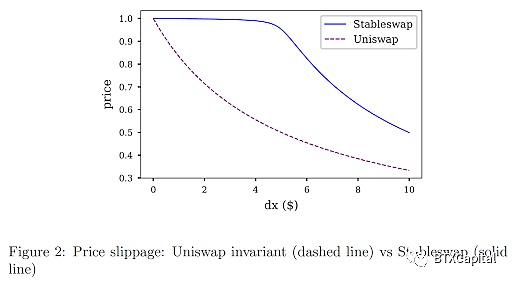
與 CPMM 相比，StableSwap 做市商受壓、 以x + y = 常數方向壓平。這確保交易價格接近或等于 1，在平衡點附近有非常小的滑點（當池中的一個代幣不接近幾乎售罄時）。當池中的一個代幣幾乎售罄時，價格開始急劇下降。這很容易理解：函數的曲率/滑點被集中/推到別處，以確保在平衡點附近的低滑點。

該模型中的 CPMM 和動態權重被用于懲罰提前知道消息的大額訂單，防止池中的代幣被完全售罄。

HUBDex 自動做市商（AMM）閃兌（Swap）功能正式上線:據官方消息，CoinXP交易公鏈為去中心化交易所HubDex提供“閃兌”工具SDK，本周HUBDex率先上線自動化做市商（AMM）的去中?化數字貨幣閃兌新功能。目前支持BTC-USDT/ETH-USDT/HUB-USDT數字貨幣之間的閃兌。

據悉，HUBDex的用戶除了可以進行交易外，還可以通過提供流動性而獲取收益。基于AMM 模式的DEX只需使用錢包連接就可進行交易，便捷性已超過中心化交易所。在資金安全方面，由于始終都是在自己的錢包中存放著的，交易所并沒有托管我們的資產，所以也不用擔心跑路的風險。[2020/11/11 12:21:30]

優點：通過添加CSMM和CPMM以及動態權重，Curve的StableSwap 實現了非常小的滑點，非常適合穩定幣。

缺點：價格始終錨定在1。如果市場價格與流動性池價格顯著不同，流動性池將被買空。因此，StableSwap 僅適用于穩定幣。

Curve V2 的動態權重、可定制的價格錨定和平滑的價格過渡：

為了確保更平穩的價格過渡和可定制的價格錨定，Curve11 V2 將動態權重 χ 修改為 K，如下所示：

Curve11?V2

Automatic market-making with dynamic peg

https://curve.fi/files/crypto-pools-paper.pdf

K0 在 0（流動性池不平衡）和 1（平衡點）之間變化，χ 和 K（以A 歸一化）作為 K0 的函數繪制如下：

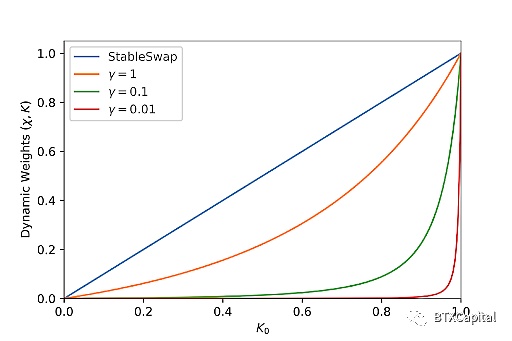
我們可以從上圖中了解Curve V2 如何使價格轉變得平滑。它實際上使動態權重在遠離平衡點時迅速下降。γ值越小，下降越快。使動態權重快速下降到零本質上相當于強制函數表現得更像 CPMM，即使流動性池只是有一點不平衡。

DW 在 twitter12 上發布了一條很棒的推文，解釋了相同的概念。

SBF：Serum首個自動做市機制Serum Swap已啟動:10月 28日，FTX創始人、Serum顧問Sam Bankman-Fried（SBF）宣布Serum上首個AMM（自動做市機制）Serum Swap已啟動，并開啟流動性挖礦。[2020/10/28]

DW?在?Twitter12的推文

https://twitter.com/dken_w/status/1422623679150649345

價格過渡問題得到了解決。現在我們討論 Curve V2 如何實現其他不是1的價格錨定。有一個價格錨定（他們在白皮書中稱之為價格標度）意味著在做市曲線上存在一個平衡點，在平衡點處按價格標度縮放的代幣數量相等：

Curve V2 在 2 代幣池中的做市商函數：

縮放后的代幣數滿足與 StableSwap 類似的等式。以最簡單的 2幣流動性池為例，做市商函數可以用 A、γ、p、D、x、y 表示。該函數可以簡化為關于 x, y 的三次函數（關于 D 的六次函數）。

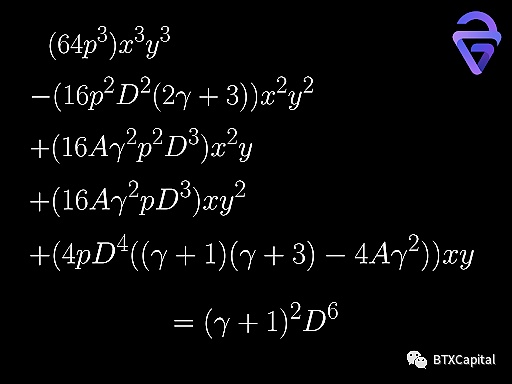
該函數的典型值圖如下所示：

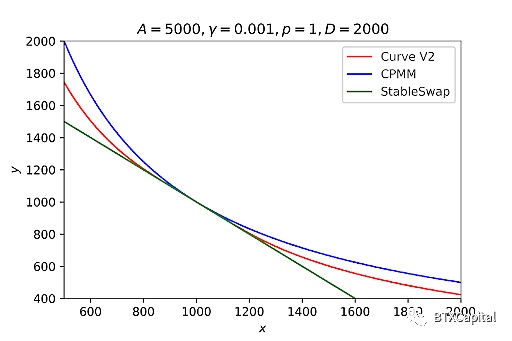
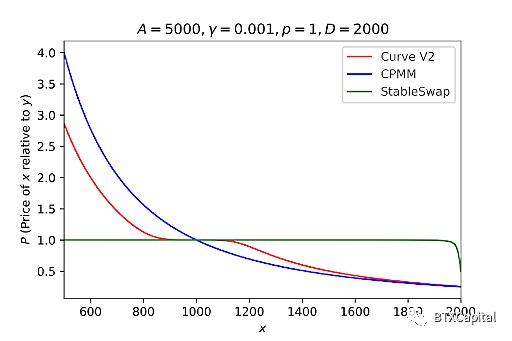
與CPMM和StableSwap相比，Curve V2的價格函數：

也可以繪制代幣 x 相對于代幣 y 的價格曲線。在平衡點 (1000, 1000) 附近Curve V2 價格函數恒定。與 StableSwap 相比，Curve V2 略微延遲了價格變動，而不是完全延遲。與 CPMM 相比，隨著交易量的增加，價格開始以較小的滑點做出反應。總而言之，Curve V2 在平衡點附近實現了非常小的滑點，并且在其他區域比 CPMM 實現了更好的滑點。至于其他非1的價格錨定，我們只需更改上面三次/六次方程中的 p。因此，錨定價格的問題也解決了。

流動性挖礦項目Cream推出自動做市商CreamY:流動性挖礦項目Cream今日發推宣布，推出資本高效（Capital Efficient）的動態AMM（自動做市商）CreamY。creamY允許：動態池（Dynamic pool）更新；收益穩定的資產；整合流動性以避免分散的資金池；單面流動性。creamY將與穩定幣、BTC和ETH交易所一起推出，CREAMY LP獎勵也即將推出。[2020/9/20]

我們可以使用類似的在StableSwap中的牛頓法來計算交換結果。首先，我們根據池中當前的代幣數量計算 D（這次使用牛頓法，因為方程要復雜得多）。其次，如果我們想換出代幣 i，我們再次使用牛頓法來求解 x?。同樣，x?的差異（按其價格標度歸一化）將是我購買的代幣數量（所有 x? 都是按價格標度縮放的代幣數量）。

為了確保多項式函數的根可以在設定的gas上限內求解，Curve白皮書討論了他們選擇的起始猜測，以及函數中的參數。他們使用一種稱為模糊測試（假設框架）的方法來確定這些最佳值。目前，我們不知道有關此方法的任何詳細信息，并且很想了解更多信息。

價格重錨過程：Xcp 標準、EMA 價格預言機、相對價格變化步長 s：

為了確保小滑點（在平衡點附近交易）， Curve V2通過改變價格標度不斷重錨做市商函數。然而，價格重錨可能導致流動性提供者承受價值損失。Curve V2 引入了一個名為 Xcp 的變量來緩解這個問題：

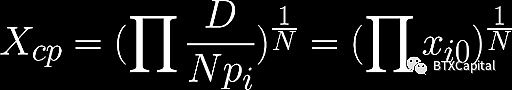
如果一次重錨后的損失大于累積的 Xcp 的一半（原始 Xcp 增加的價值），則該算法將保持做市商函數不變。有幾個問題我們想在未來回答，因為白皮書只簡要討論了 Xcp。查看其源代碼可能會有所幫助。

Xcp 值是否與用流動性池中當前代幣數計算出的價值成正比？

存入或取出流動性是否計入 Xcp？

如果取出流動性計入Xcp，如果Xcp減少幅度過大會阻止取出流動性嗎？

對于價格重錨，Curve V2 使用 EMA（注：指數移動平均線）價格預言機來確定預言機價格。新的預言機價格向量由最近一次交易價格向量和前一個預言機價格向量的線性組合確定。新價格標度向量的變化方向與預言機價格相似，但不完全等于新預言機價格。他們通過引入相對價格變化步長 s，將價格標度向量滯后于預言機價格。該方程可以使用歐幾里得幾何輕松導出。EMA 價格預言機和價格標度延遲是為了減少近期價格波動的影響并更好地代表長期市場價格。

Messari前主管：無法相信自動做市商是一種范式轉變:8月17日，Messari前主管、股票及加密貨幣交易員Qiao Wang發推稱，Uniswap很酷，它是我們等待區塊鏈擴展時的絕佳臨時解決方案。但是我無法相信人們實際上是在說，像自動做市商（AMM）這樣的東西是一種范式轉變。[2020/8/17]

關于相對價格變化步長 s，根據我們“刷新Curve官網”的經驗，部分流動性池的 s 變化頻率至少為十分鐘的量級以上。Curve V2 如何更新 s 是一個有趣的問題，超出了我們當前知識的范圍。查看其源代碼也會有所幫助。

下面顯示了一個演示一次價格重錨過程的圖：

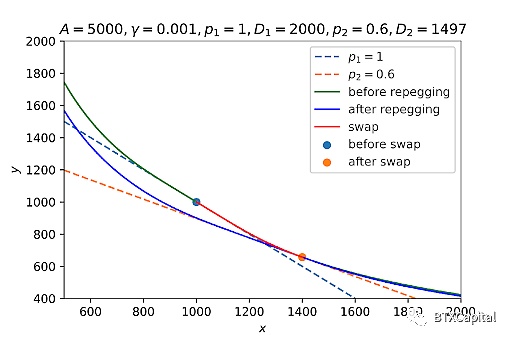
假設我們在 x = 1000 開始我們的交易，并在 x = 1400 結束我們的交易。最初，價格錨定于1 。交易后，價格移動到 0.6。為簡化起見，僅出于演示目的，我們將新的價格標度設置為與現貨價格相等（價格現在錨定于0.6），并求解六次方程以獲得 D。現在做市商函數錨定于 0.6，如上所示。

價格重錨本質上相當于找到一個新的做市商函數，該函數穿過當前代幣數量位置（在 2 代幣池情況下為 (x, y)），在 (x0, y0) 處有一個平衡點，使得 y0/x0 為 等于 (x0, y0) 處導數的絕對值。一個有趣的課題是獲取真實的Curve流動性池參數，做一個更好的（可能是動畫）價格重錨過程的演示。

Curve V2的動態交易手續費：

由于上面討論的Curve V2 的做市商特性，將交易費用設為2級交易費用與動態權重的線性組合是合理的，衡量我們離平衡點有多遠（當前價格變動是否更像是 StableSwap 或 CPMM）。Curve V2 選擇的 fmid 和 fout 值分別為 0.04% 和 0.4%。下圖展示了 2 代幣池中的費用如何變化（假設沒有價格重錨或流動性變化）：

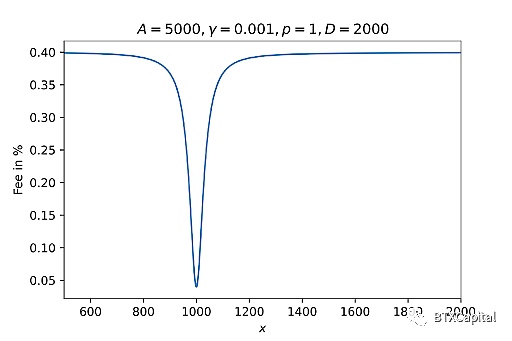
優點：做市商函數可以錨定于任何價格，適合所有代幣，而不僅僅是穩定幣。價格過渡比 StableSwap 更平滑。Curve V2還根據其內部的價格預言機不斷更新價格標度，以更好地代表市場價格，確保在平衡點附近交易。動態費用確保在此基礎上提供甚至更好的價格。

缺點：由于求解三次方程和六次方程，Gas 費用可能會更高。僅根據其內部價格預言機進行價格重錨可能存在風險。我們想知道在通過 Xcp 標準時，是否存在價格標度與市場價格明顯不同的情況。如果是這種情況，與其他預言機交叉檢查價格可能會有所幫助。

Curve 的 StableSwap 和動態錨定 V2 是為了使交易滑點盡可能小。StableSwap 始終錨定于 1，而 V2 使錨定價格跟隨市場價格。

下面將討論 AMM 算法的一些最新進展和可能的改進。

DEX聚合器：Balancer SOR算法的通用解決方案：

DEX 聚合器是聚合現有 AMM 協議以實現更好交易結果的協議。如上所述，Balancer 的 SOR 算法也適用于 DEX 聚合器，以確保數學上最優的交換策略。

Balancer 的 SOR 算法的一般解決方案，沒有任何價格函數近似，可以表示如下：

因為價格函數可以是任何形式，具體取決于生成它們的 AMM 算法。這意味著滿足總代幣數量守恒和相等最終價格等條件的方程可能沒有解析解。

因此，我們引入了一種在機器學習等領域常用的技術，稱為梯度下降。我們將損失函數定義為不同價格函數值的方差。在選擇一個起始猜測（一個簡單的、不知情的猜測可以是每個池中的交易量相等 N/n）后，我們可以迭代（通過損失函數相對于該變量的偏導數改變每個交換量，乘以學習率 l) 以獲得最佳結果，在一定的誤差接受范圍內。

由于作為最終等價函數的總交易量是單調的，因此該方法應該能夠找到全局最小值（方差 = 0）。同樣，上面的計算假設沒有簡單的解決方案（沒有價格函數總是大于或小于范圍 (0, N) 上的其余價格函數）。

Pivot 算法：解決無常損失問題的一種嘗試：

Pivot 算法試圖通過使做市商函數經過一個固定點 (x0, y0) 來對其進行樞軸旋轉。

(x0, y0) 處的價格將始終是設計的當前市場價格 Pt。這在概念上確保套利總是將流動性池帶回到點 (x0, y0)。由于此功能，無常損失將為零。然而，實際上，該算法沒有足夠的參數來擬合當前儲備（x，y）和（x0，y0）。這意味著我們必須等待流動性池回到 (x0, y0)，然后更改做市商函數。

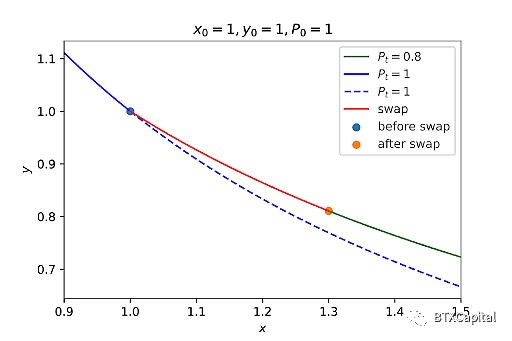
從上圖中我們可以看出，交易后的點不在新的做市商函數上（藍色和藍色虛線）。如果當前市場價格低于當前儲備的現貨價格，則流動性池也可能沒有任何動力回到 (x0, y0)。

我們想知道是否存在這樣的函數通過 (x, y) 和 (x0, y0) 以及在 (x0, y0) 處的可調導數來適應市場價格。如果我們假設函數是凸的，那么市場價格不能小于這兩個點之間的線性段斜率。因此，如果做市商函數必須是凸函數，則此問題可能沒有完整的解決方案。

單邊流動性解決方案：

流動性提供者在存入流動性時可能不方便存入所有類型的資產。我想知道是否存在與 Bancor 采取的彈性供應方法不同的其他機制。直覺上，有兩種解決方案：1. 首先使用相同的協議交換部分代幣 2. 無論如何存入單邊流動性，讓套利將價格帶回市場價格。

例如，我們希望將流動性存入一個等值的 2 代幣池中。

我們只有代幣 x。不難計算我們需要交換多少，以便交換后每種代幣的價值相等。也很容易證明 β 總是在 0 和 1 之間，這意味著一個合理的結果。但是，交易后的價格可能與存入流動性時的價格不同。因此，我想知道協議是否真的將交換和流動性存入作為一項原子操作。進行交易時也存在價格滑點。到目前為止，Balancer 和 Curve 等協議如何處理單邊流動性存入仍然是我們的一個問題。如果滑點很小，則進行上述操作是合理的。

Balancer and Curve 白皮書中描述的第二種方法是是直接存入單邊流動性。這可能會大大改變價格。由此產生的套利也可能使無常損失變得重大。我們個人在 Balancer 白皮書和文檔中沒有看到任何懲罰措施。另一方面，Curve 在存入單邊流動性時引入了一種稱為不平衡費的東西，其范圍從 0% 到 0.02%。在現實中，由于套利和無常損失，在第二種方法下存入單邊流動性并沒有真正的動機。

了解更多與單邊流動性相關的其他創新將會很有趣。

由于本論文過長，?AMM 算法的一些最新進展和可能的改進及后續內容將于下篇 公布。

原文鏈接：https://link.medium.com/ynEydZUihjb ? ? ?

作者：Leo Liu, Guangwu Xie

翻譯：Vanessa Cao

校對：Leo Liu, Guangwu Xie

排版：Jane Hu

感謝：Fangyuan Zhao, Showen Peng, DW, Lianxuan Li, Dave White, Dan Robinson, Vanessa Cao, Jane Hu

Tags：CURCurveSWAPSTAcurve幣價格PAXCURVEChilliSwapHest Stake

中幣下載